Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#51 Re: Help Me ! » Transformations » 2015-01-07 11:41:37
I see! So, in general, how should I proceed with a question like this? Matrix algebra seemed the best way, simply because it's the way I'm familiar with!
#52 Help Me ! » Transformations » 2015-01-07 07:38:03
- Au101
- Replies: 17
This time, I was confident:
24. Under a certain enlargement (3,4) → (0,-2) and (-5,2) → (4,-1). Find the image of (-3,-8) under this enlargement.
Now, I'm a little rusty, so I looked up the form of the matrix for the "scaling" transformation and found:
Gives a scaling by k in all directions.
I tried this, but my answer was wrong. Then I thought: 'hey! maybe the scaling isn't the same in both directions,' so I tried instead:
Still wrong. Then I realised: 'oh! the centre may not be (0,0),' so I tried:
Still wrong. Then I thought: 'well, what if the x and y coordinates of the centre of enlargement are different?' So that was when I had my last try:
Running the numbers gives me:
But:
Does not give the right answer.
So my question for the good folks at mathisfun is: who's wrong - me, or the book? ![]()
#53 Re: Help Me ! » Cones » 2015-01-07 02:44:45
What a lovely, comprehensive explanation, thanks! ![]()
#54 Help Me ! » Cones » 2015-01-06 16:02:07
- Au101
- Replies: 2
Hey, me again.
I can't decide whether this is something I've never done, or something I've forgotten, so let's just dive straight in with the question.
22. A plane intersects a right-circular cone and is parallel to the base of the cone. If V is the vertex of the cone and VA the altitude, then let B be the point where the plane cuts VA. It it given that VB:BA = 3:2. Are the following statements true or false?
(i) The ratio of the volume of the small cone (the upper part of the section) to the volume of the whole cone is 8:27.
(ii) The ratio of the surface area of the small cone to the surface area of the whole cone is 9:25.
(iii) The ratio of the volume of the small cone to the volume of the frustum of the cone (the lower part of the section) is 27:125.
Now, I dare not even try to draw this, but I'm pretty confident I do know what the question means. You've got your standard cone, where the "top" (here, I believe, referred to as the 'vertex', though I believe 'apex' is also used) of the cone is directly above the centre of the base. The top of the cone is labelled V and we extend an imaginary line from the top of the cone to the centre of the base, which we'll call A. This line is VA - the "altitude" (i.e. the height of the cone, i.e. the distance from the base of the cone to the point at the top). Now, at a point B along this line a plane cuts the cone into two parts. So we're left with a "small cone" and a "frustum". Now, the ratio of the height of the small cone (VB) to the height of the frustum (BA) is 3:2. This means, then, that the height of the small cone (VB) is 3/5 that of the whole cone (VA) - am I right?
Now, what else do we know. Well, we know the volume of a cone is:
Where r is the radius of the base and h the height of the cone. So we know that for the whole cone h is VA and we know that for the small cone is 3/5VA.
What I don't know is what either of the radii are and I don't know how to work out in what proportion the radii are, which I imagine is important.
I'm also not really sure how to proceed on the basis of this information. What I jotted down is this:
Which I can kind of see makes (i) false (book says it is indeed false), but I don't really understand why - I couldn't explain it to anybody if they asked. I then looked at the next one and, yeah, apparently it's true, but I don't really know why it's true. One of the things that's stalling me is the fact that I'm not sure whether I'm supposed to worry about the radii and - if I am - how I can work out what ratio they're in ![]()
#55 Re: Help Me ! » Arithmetic modulo » 2015-01-06 04:06:42
Okay, I see it now, thank you! ![]()
#56 Help Me ! » Arithmetic modulo » 2015-01-05 13:24:19
- Au101
- Replies: 3
Hey ho, I've come up against a question on something that was never actually on my syllabus, so I don't really know where to begin. I googled around looking for things on modular arithmetic and the modulo operation, but I can't apply it to this question, because I can't really parse the question, I don't understand what it wants.
Here it is:
21. Write down all the solutions of 3x(3x + 4) = 0
(i) in arithmetic modulo six; (ii) in arithmetic modulo five.
Obviously the "basic" solutions are x = 0, x = -4/3, but I don't really know what to do with those numbers
#57 Re: Help Me ! » A funny question » 2015-01-05 09:56:41
Thank you both very very much ![]()
#58 Re: Help Me ! » A funny question » 2015-01-05 07:49:35
Hmmmm, well, that's what I took "illustrate the following sets on the same diagram" to mean, but if you think we just need the elements of the set:
Then it should be easy enough to work them out, I get:
#59 Re: Help Me ! » A funny question » 2015-01-05 07:22:25
Well indeed, now comes the tricky bit - I assumed I was supposed to convert all of this lovely (hard-earned ![]() ) information into a Venn diagram. And this is where Au101's brain goes: well forget that, I'm off for a cup of tea!
) information into a Venn diagram. And this is where Au101's brain goes: well forget that, I'm off for a cup of tea! ![]()
Er, this is what I have, assuming I've done this uploading an image thing right ![]()
On second thoughts, how does one upload an image ![]()
Let's try:
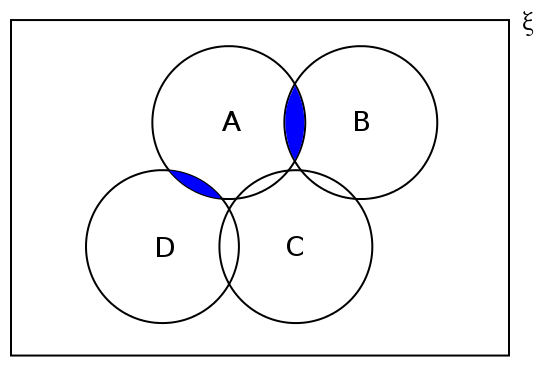
#60 Re: Help Me ! » A funny question » 2015-01-05 06:36:29
Ooooh that's lovely, and now I see it all laid out nicely I can see how I was wrong about D in that A and D will only have two members in common - one on each of the lines, because of course, they must be tangents to the circle that is the locus of A. The points I suggest as elements of D came from choosing the point (0,0) (which is on the line x = y).
I proceeded as follows: The perpendicular distance between the point (0,0) and the line D1 is 1. Thus we can draw a right angle triangle - can we not? - with hypotenuse 1 and the other two sides of length a:
By inspection it is clear, then, that the point on D1 which is 1 unit from (0,0) is (-1/√2, 1/√2).
#61 Re: Help Me ! » A funny question » 2015-01-05 04:52:37
Oh, sure, okay ![]() Thanks
Thanks ![]()
Well, if we were to show B on a graph it would obviously be a straight line with equation x = y. So, the gradient is 1 and the y-intercept is zero. The set B will also be infinitely large, but some members of that set will be the point (0,0), the point (1,1) (i.e. Q), the point (2,2), etc.
Now, C doesn't seem that hard either. On a graph it will be a straight vertical line with x = 2. So it is also infinitely large, but includes the point (2,0), the point (2,1) and the point (2,2).
Now, D is less generous, but I believe, on a graph, the locus would be two lines parallel to x = y. One of the lines will be at a distance of 1 unit from x = y to the "left" (x < y) and the other will be at a distance of 1 unit from x = y to the "right" (x > y). Obviously another infinitely large set. Not 100% sure but I think a couple of points in this set would be:
So, it seems to me that: A and B will have two members in common, since the straight line that is the locus of B passes through the centre of the circle that is the locus of A.
B and C will have one member in common: the point (2,2).
A and C will have one member in common: the point (2,1).
There is no element common to all of A, B and C.
The two lines which form the locus of D will cross the line x = 2 at one point each, so the C and D will have two members in common.
B and D can have no members in common.
A and D will, I think, have four members in common - two on each of the lines which form the locus of D.
I don't think there will be an element common to all of A, C and D.
Now, how to draw that? Assuming I'm right!
#62 Re: Help Me ! » A funny question » 2015-01-04 16:16:25
Sure, unless I really have forgotten everything! If we were to show it on a graph we would have a circle centre (1,1) (i.e. Q) with radius 1. The set A will therefore be infinitely large, but some members of that set will be the point (1,2), the point (1,0), the point (2,1) and the point (0, 1).
#63 Help Me ! » A funny question » 2015-01-04 12:54:44
- Au101
- Replies: 13
In a style I've never seen before. I'm not really sure where to begin with this one. I had a go, but by the time I got to part (v) I was just scratching my head really:
They don't seem to write questions like that anymore! ![]() Does anybody know what they're looking for here (no answer provided).
Does anybody know what they're looking for here (no answer provided).
#64 Re: Help Me ! » Parallelograms » 2015-01-04 07:11:40
Ooooh yes that seems about right, thank you both of you!
So, to prove this, I should presumably show that AB = CD and AD = BC. Should I also show that BD is perpendicular to AC?
#65 Help Me ! » Parallelograms » 2015-01-04 04:05:51
- Au101
- Replies: 5
Just another one to check whether or not I'm being silly. The question is:
Given that the points A, B, C, D have coordinates (5, 6), (-2, 4), (-5, 5), (2, -3) respectively, prove that ABCD is a parallelogram.
Surely ABCD is not a parallelogram?
I wonder whether the point at (-2, 4) should really be at (-8, -4). (Although, in that case, (-5, 5) should surely be B and (-8, -4) C, if we're going to talk about the parallelogram ABCD.)
#66 Re: Help Me ! » Direct Proportionality » 2015-01-04 04:01:20
Thanks for the confirmation bob bundy! ![]()
#67 Help Me ! » Direct Proportionality » 2015-01-03 04:56:45
- Au101
- Replies: 2
Hello again everyone at mathisfun, happy new year to you all ![]()
As part of my attempts to get the new year off to a good start, I've been brushing up on some old, secondary level maths I've now completely forgotten! (All of which makes me feel rather silly! ![]() )
)
I'm rather stuck on the following question:
So, 'no problem,' I thought:
"Right you are!" Says the book. 'Great!' I think, let's move on:
I calculate my values to complete the table based on that and come up with:
While the book has:
Can anybody see where I've gone so wrong?
Ta!
#68 Re: Help Me ! » Integration by parts question » 2014-08-25 08:14:40
I see, I now understand why wolfram gave me the answer it did. I had wondered whether it might be because wolfram uses complex values as well, but until you explained I didn't know how to get it to only use real values of x - thanks! ![]()
As for the integration by parts, I suppose I will just have to do a little more practise so that I can spot what to do. Thanks again ![]()
#69 Help Me ! » Integration by parts question » 2014-08-25 07:05:28
- Au101
- Replies: 3
Having moved on to integration by parts, I've found myself stuck on another question:
I have two problems here. My first is that I get the answer:
Whilst the book gets:
That's no problem, I thought, because:
But when I checked whether this was true in WolframAlpha, it told me that it was false, so I was wondering whether my answer was, in fact, equivalent to the one in the book or not?
My second problem is that I came by this solution by adapting a worked example of
Which I found online.
I did it by setting:
But the problem I have is that I don't really understand why that is the thing to do. In all of the other examples in my book, I've had a product of two functions of x (often f(x) = x). I have then selected one of the functions of x to be u and integrated the other function of x. The result of the integration I then set as v. Here I've got something totally different and the book offers no guidance, unfortunately, so I was wondering if anyone could explain how this works as I may well have similar problems in future.
#70 Re: Help Me ! » Proof Check » 2014-08-23 04:22:59
Oh N.B. for anyone who didn't follow:
I believe. Hence step 3.
#71 Re: Help Me ! » Proof Check » 2014-08-23 04:19:23
Then:
#72 Re: Help Me ! » Proof Check » 2014-08-23 04:16:16
Hi bob bundy, suppose we reason thus, based on what we proved before:
#73 Re: Help Me ! » Proof Check » 2014-08-21 10:54:39
Thanks! ![]()
There's actually a second part of this question and, sadly, I'm totally stuck on that too!!
I reckon this could be done quite easily with integration by parts, but in the textbook this is the last question in an exercise on integration by substitution. Integration by parts is actually the next subsection, so I'm wondering if there's another way?
I don't even know where to start with this. I tried using what I just proved, but it doesn't seem to help - at least not in the very first place. I imagine I'll be able to use it after finding the first integral, but I can't seem to use it to do anything useful to the first integral, since
There's nothing that I can think to substitute.
I did do some algebra to get:
But that does nothing about the x it's multiplied by.
Does anybody have any ideas?
#74 Help Me ! » Proof Check » 2014-08-20 12:35:44
- Au101
- Replies: 6
The last question on integration by substitution in my books asks for a proof. I think I've got it, but obviously the proof's not given in the back, so I could be talking absolute nonsense. I was wondering, therefore, if someone could give it a look over and tell me if I'm right in my approach.
Here's the question:
My approach was as follows:
#75 Re: Help Me ! » Difficult partial fractions and/or difficult integral » 2014-08-20 02:19:14
Certainly, thanks a lot ![]()