Math Is Fun Forum

Alright that's good to hear! Last 5:

16. If a radius bisects a chord, then the lengths of the parts of the radius on either side of the chord are equal. - I would go with 'C'
A Given
B Definition of a chord
C unfounded
D Definition of supplementary angles
E Definition of a bisector
F Definition of radius

17. If a circle has a central point M, and both point A and point D are on the circle, then ls_MA and ls_MD will be equal. - I'm thinking of 'E' on this
A Given
B unfounded
C Definition of a line segment
D Definition of supplementary angles
E Definition of a bisector
F Definition of radius

18. If I have two points, (-2, -3) and (-4, 4) then the distance between them is sqrt(53). - I'll go with 'C'
A Distance Formula
B Definition of a point
C Definition of a distance
D Definition of a line
E Definition of coordinates
F Definition of radius

19. The given points (4, -8), (4, -5), and (-2, -6) make a right triangle. - I choose 'D'
A Distance Formula
B Definition of a right triangle
C Definition of a triangle
D unfounded
E Pythagorean Theorem
F Definition of radius

20. The given points (2, -3), (-7, -7), (2, -7), and (-7, -2) make a square. - I think 'F' would be the answer
A Definition of coordinate
B Pythagorean Theorem
C Definition of a square
D Definition of supplementary angles
E Distance Formula
F unfounded

Alright so #15 my new answer will be 'E'. As for #14, I am starting to reconsider my answer, I was thinking of 'D'.

8. In the figure above, the measure of angle AMC is 90 degrees. - So new answer would be 'A'? I said 'C' because not enough proof/information was given to support the answer.
A Given
B Definition of radius
C unfounded
D Definition of an octagon
E 1267200 inches
F Definition of supplementary angles

9. In the figure above, the measure of arc AC is 90 degrees. - My Answer is C - answer 'A' says that the measure of an arc is equal to the measure of the angle that subtends it, which is not always true. The arc can be of different lengths sometimes. But in THIS case, would 'A' be the correct answer?
A The angle measure of an arc is equal to the measure of the central angle that subtends it.
B 126498 inches
C unfounded   
D Definition of an octagon
E Definition of supplementary angles   
F 1267200 inches

10. In the figure above the measure of angle AME is x degrees, then the measure of angle EMB is 180-x degrees. - So my new answer would be 'D'? Now that I think of it, it does seem like two supplementary angles. Since the image is a circle I guess I wasn't expecting them to implement supplementary angles into it.
A Given
B unfounded
C Definition of an octagon
D Definition of supplementary angles
E 1267200 inches
F Definition of radius

Cool! On to the next 5:

The follow questions #6 - #10 will be using this picture:

6. In the figure above, line segment MC is equal to imaginary line segment MI. - My Answer is F (does not exactly explain, so I choose 'F' instead of 'A')
A Given
B unfounded
C Definition of supplementary angles
D 1267200 inches
E Definition of an octagon
F Definition of a circle: all points are equidistant from the center

7. In the figure above, line segment EJ is equal to line segment JM - My Answer is B (not enough information or proof is given)
A Definition of radius
B unfounded
C Definition of an octagon
D 1267200 inches
E Given
F Definition of supplementary angles

8. In the figure above, the measure of angle AMC is 90 degrees. - My Answer is C (not enough information or proof is given)
A Given
B Definition of radius
C unfounded
D Definition of an octagon
E 1267200 inches
F Definition of supplementary angles

9. In the figure above, the measure of arc AC is 90 degrees. - My Answer is C (i thought about 'A' but then realized that this is not always true, the arc may be shorter or longer than the central angle that subtends it [for example the 'EA' arc])
A The angle measure of an arc is equal to the measure of the central angle that subtends it.
B 126498 inches
C unfounded   
D Definition of an octagon
E Definition of supplementary angles   
F 1267200 inches

10. In the figure above the measure of angle AME is x degrees, then the measure of angle EMB is 180-x degrees. - My Answer is A (proof is given for this one which led me to choose 'A - Given')
A Given
B unfounded
C Definition of an octagon
D Definition of supplementary angles
E 1267200 inches
F Definition of radius

It looks like a tall diamond. If cut in half, it can make two triangles.

2. Now do the same with this list, and describe the shape. - I said E (previous question asks the same thing and I said it looks like a rhombus, which was right, this one is telling me to describe it [in other words, describe what a rhombus looks like] but I'm not exactly sure which triangle would best describe it)

(0,-1), (0,3), (1,1), (-1,1)
A A square
B Two acute angles that meet at the acute angles
CA triangle
D Two right triangles that meet at the right angles
E A rhombus
F Two obtuse triangles that meet at the hypotenuse

I would say for this one - F

By the way, my teacher replied for the previous math lesson and got 10.000!

Alright, I sent in the lesson and now I am waiting for the reply which may take a little time. While that is being checked, I did another lesson and got 17 out of 20. Here are the three I got wrong along with the answers I put:

I need to put these points on a graph to answer the questions.

1. Draw a Cartesian Coordinate system for yourself, and then determine whether these sets of points form triangles - I said F

Set 1: (0,0), (1,1), (0,1)
Set 2: (-1, 0), (1,1), (3,2)
Set 3: (0,0), (5,0), (3,5)
A set 1 line segment, set 2    Triangle, set 3 line segment
B set 1 Triangle, set 2    Triangle, set 3 line segment
C set 1 Triangle, set 2 line segment, set 3 Triangle
D set 1 line segment, set 2 line segment, set 3    line segment
E set 1 Triangle, set 2    line segment, set 3 line segment
F set 1 line segment, set 2 Triangle, set 3 Triangle

2. Now do the same with this list, and describe the shape. - I said E (previous question asks the same thing and I said it looks like a rhombus, which was right, this one is telling me to describe it [in other words, describe what a rhombus looks like] but I'm not exactly sure which triangle would best describe it)

(0,-1), (0,3), (1,1), (-1,1)
A A square
B Two acute angles that meet at the acute angles
CA triangle
D Two right triangles that meet at the right angles
E A rhombus
F Two obtuse triangles that meet at the hypotenuse

3. (-1, 0), (2, 0), (2, 4), and (-1, 4) - I said B (this question is asking what shape do these points make. I said square but I guess this is more of a RECTANGLE so I would say A)
A a rectangle
B a square
Ca parallelogram
D a rhombus
E a triangle
F a line segment

Oh alright, I see the images on the Wikipedia.

For the Surface Area.

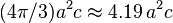
For the Volume.

Two questions:
First, what does the letters 'e' and 'c' stand for?

Second, so after finding the major axis (a) and the minor axes (b), I can do the equation?

I am starting to get confused as to what methods to use to get the area and volume of the football. Now that I see it, the Prolate Spheroid does resemble the football best. I have never done measurements based on this shape and therefore don't have enough knowledge on how to get the answers (although they might not be accurate, but close). I have found a picture online and came up with another idea. Look at the picture below and see how it is cut up into 4 triangles similarly to what you could do with a perfect circle.

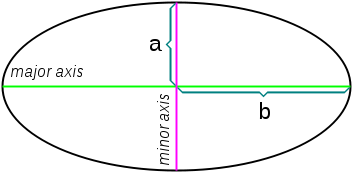
This is my idea on how to get the answers. I would trace the football in a piece of paper and similar to the image, I would draw two lines forming width and height. I would then use measurements finding the slant height, height (pink line as seen on image) and width(green line as seen on image) of the football. Am I going the right way with this so far? Kind of tough for me to figure out what to do. I would appreciate some help understanding what to do and how to do it.

7. Problem solver (worth 4 points): Come up with a way to find the area and volume of a football. Include in your answer a way to acquire any necessary measurements without cutting or otherwise destroying the football. Also include all necessary formulas to implement your idea. (You don't need to find actual numbers, just outline the method in step by step detail--think of all the measurements you'll need to acquire and how you'll get them.)
Answer:
I need to find the area and volume of a football without destroying the ball. To do this, I would first start with measuring the ball from top to bottom. I would mark a line exactly on the middle of the ball. Once I have done that, I'll use paper to cast a mold on exactly half of the ball. I will then take it off to have a half football mold which would look like a cone. With this cone, I would find the measurements required to fit into these two equations:

T = (PI)rs + (PI)r^2 - for the cone area
V = (1/3)(PI)(r^2)h - for the cone volume

One I have gotten the answer for each equation, I will simply just x2 both of them to find the final answer of what the volume and area of the football is.

3. If a hexagon has a radius (center to point of angle) of 6, what is the side of the hexagon?
Answer: 6
If the radius is 6, so are the sides.

NOTE: i have edited my first post for #4 but it seems as if you quoted my text BEFORE I edited them. See my new answer:
4. If a hexagon has a radius (center to point of angle) of 6, what is the area of the hexagon?
Finding the area of ONE triangle:
r^2 sqrt3 /4
6^2 sqrt3 /4
36 x sqrt3 /4
36 x .433021
15.588756

a = 6 x 15.588756
Answer: 93.53