Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#26 Re: Help Me ! » The chain rule » 2015-01-24 11:59:09
With my simple functions
x = 2t so t = (x/2)
Therefore y = (x/2)^2
It would be somewhat harder with the functions you chose.
Bob
Yes 
I see that, so we can see that since both x and y are functions of t, there will be some way of relating x and y. They are both expressed in terms of t so what we can do is express t as some new function of x and thereby express y in terms of x (since y is a function of t and we have just expressed t as a function of x, so y may also be expressed as a function of x.) Clearly, in some cases y will have to be expressed as a function of x and t.
#27 Re: Help Me ! » The chain rule » 2015-01-24 11:52:40
I see - I think, but I feel like I'm missing something deeper. It's like I'm almost there with it, but not quite. I can see that where you have the points:
You can say that the gradient (say m) is given by the change in y over the change in x. That is to say:
And that δx and δy must both be functions of t, but I guess I'm not quite sure I see why the gradient of the graph y = φ(x) is equal to gradient of the graph y = g(t) divided by the gradient of the graph x = f(t). It feels kind of right and yet, I don't see it somehow.
Edit: obviously that should really be the gradient of the curves at an equivalent point - it's actually not very easy to express!
#28 Re: Help Me ! » The chain rule » 2015-01-24 11:46:04
So we're saying that we can definitely see that y may be expressed as a function of x, although quite what that function would be I don't know - a function in terms of t, it seems.
#29 Re: Help Me ! » The chain rule » 2015-01-24 11:44:22
but I wouldn't want you to stay up on my account!
I've just driven 70 miles round the M25 so my brain is wide awake, even though I'm theoretically tired having spent the day doing jobs for my Mum. So this is probably a good way to unwind.
Bob
Ooooh 
I have mostly bad memories of the M25 
#30 Re: Help Me ! » The chain rule » 2015-01-24 11:43:21
The points, by the way, would then be (13, -5) and (64, 7). I think, sadly, we ended up talking past each other just a little bit, but it doesn't seem to have mattered too much because I got the last message
#31 Re: Help Me ! » The chain rule » 2015-01-24 11:39:16
But for now I shall let t = 1 and 2, if that works nicely?
#32 Re: Help Me ! » The chain rule » 2015-01-24 11:38:16
I'm still with you if you're here, but I wouldn't want you to stay up on my account!
#33 Help Me ! » The chain rule » 2015-01-24 08:01:25
- Au101
- Replies: 16
Hi, I'm having a little difficulty understanding the presentation of the chain rule in my textbook. Here's what it says:
Now, I'm having a few problems understanding this, my first problem is with the following sentence:
I'm not sure I understand why "there will be a functional relationship between x and y."
Say I try a couple of examples - just in order to see it in practise. Let's say - to take some random examples from the top of my head - we say:
Now, admittedly, I could have made my life easier for myself here, I just wanted a couple of curves, but if I look at these two curves, I really can't see any reason why there must be a relationship between x and y.
So that's my first problem which I was hoping for some help with - I was wondering if somebody might be able to unpack and explain this sentence a little for me.
The second problem I have is I'm afraid I simply can't see where:
comes from. I just don't follow and I was wondering - again - if somebody could just add a little bit more explanation so I can see why:
#34 Re: Help Me ! » Looking for confirmation of a proof » 2015-01-21 04:13:23
Yes I puzzled over that. I am sure it is true, because, well I reasoned this out in a few ways I think. First, I thought:
Second I thought:
Which implies, looking at things from the other point of view, that:
And I was about to write that I wasn't sure how to rigorously derive the statement, it just seemed intuitively true to me, but I've now realised that surely my last two lines would do the trick?
#36 Help Me ! » Looking for confirmation of a proof » 2015-01-20 07:43:23
- Au101
- Replies: 4
Question:
I have an answer to this question, but I'm not confident enough in myself to be certain that this is a valid proof. So I was hoping for some confirmation, or for somebody to tell me why I can't do what I've done. Thanks
#37 Re: Help Me ! » Bearings » 2015-01-18 08:06:16
Lovely stuff, such a great help
#38 Help Me ! » Bearings » 2015-01-17 13:29:52
- Au101
- Replies: 2
God it's been a while, but I can do the trig, I just don't seem to be able to draw this diagram correctly. I've had a number of gos, where I've thought I've had it and yet, I always end up a long way out - an order of magnitude usually.
53. From A, the bearing of X, the foot of a tower, is 041° (N 41° E) and the angle of elevation of Y, the top of the tower, is 5°. The distance AX is 1000 m. From a point B, due E of A, the bearing of X is 313° (N 47° W). A, B and X lie in the same horizontal plane. Calculate
(a) the height of the tower,
(b) the distance BX,
(c) the angle of elevation of Y from B.
#39 Re: Help Me ! » Vectors practice » 2015-01-17 05:57:46
Lovely stuff Thanks bob bundy!
#40 Help Me ! » Vectors practice » 2015-01-17 04:33:48
- Au101
- Replies: 2
Hello again.
I've tried all sorts, I've looked at it every which way I know how, I was sure I'd be able to figure this one out, but - finally - I decided it was time to move on. So, what am I overlooking here?
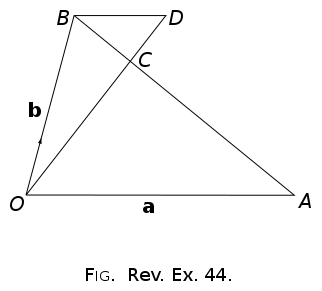
So:
...And I run out of steam. Anything else I try to do from there always leads me back to a restatement of something I've already worked out. So I thought maybe it's not about simple vector arithmetic, maybe I have to try and use the fact that it's given me a ratio to work out some other ratios, but I've not been able to make any breakthroughs. At one point I tried constructing a rectangle around the whole shape with vertices O and A as well as one directly above O at the same height as B and D and another at that height and directly above A. Finally I tried resolving b and expressing it as some vertical component x + some fraction of a, but I couldn't make any of these approaches work.
#41 Re: Help Me ! » Singular matrices » 2015-01-10 15:03:03
Thanks
#42 Help Me ! » Singular matrices » 2015-01-10 11:21:37
- Au101
- Replies: 3
det(M) = 1, is that the reason why it cannot be singular, or is there something I'm missing?
#43 Re: Help Me ! » Transformations » 2015-01-10 09:50:04
Okay, thanks bob bundy, I think we're good now!
#44 Re: Help Me ! » Transformations » 2015-01-09 08:12:20
So could I do something like this, maybe?
(Sorry. Edit:)
#45 Re: Help Me ! » Transformations » 2015-01-09 04:37:17
Oh yes Yes, I ended up with that shape, but I didn't know what to do with it! 
So what would the final answer look like? How do I
#46 Re: Help Me ! » Transformations » 2015-01-08 15:46:56
Thanks for all the help so far.
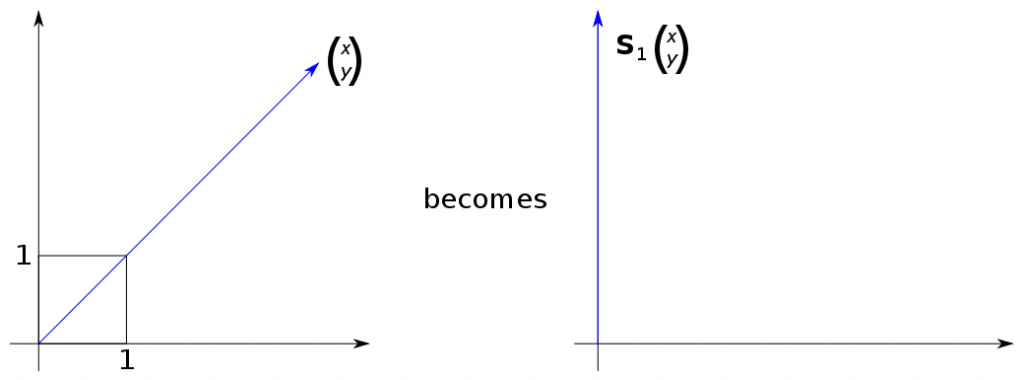
Okay, so - sorry, I've only just got a chance to work on this - I tried applying S1 to an F shape and then to a simple right-angled triangle and, well, all it did was distort my shapes! My nice right-angled triangle has been moved and the angles have changed dramatically I'm not really sure how to proceed and I'm also not really sure what the vector:
looks like, either :S
#47 Re: Help Me ! » Transformations » 2015-01-07 15:39:51
Wahey, let's have some fun with part 2 before bed
It's been a long time, I'm not entirely sure how the vector:
Would look on a diagram, but my gut reaction is that it would like the graph of y = x.
So what I did was:
Which I guess would look like the graph of x = 0?
Next I did:
Which I imagine looks like the graph of y = 2x.
Am I on the right track. I hate drawing diagrams
#48 Re: Help Me ! » Transformations » 2015-01-07 15:01:34
You're right, thanks for the help
#49 Re: Help Me ! » Transformations » 2015-01-07 12:47:33
I do agree with you about the centre of enlargement and the scale factor, though, thanks!
#50 Re: Help Me ! » Transformations » 2015-01-07 12:46:32
What do you get as the final answer? Because I get (3,4), while the book has (7,16).