Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#251 Re: Exercises » Fumble and Botch strike again. » 2009-12-27 09:26:34
#252 Re: Dark Discussions at Cafe Infinity » Are the bobbyms taking over the world? » 2009-12-24 00:25:52
I did suspect once that PowerOfPi at AoPS was the same as LuisRodg over here because they had the same avatar; now Im not so sure.
#253 Re: Help Me ! » proof of cauchy schwarz » 2009-12-23 10:26:43
Because its graph lies completely above the x-axis and does not intersect it.
#254 Re: Help Me ! » Ideals of ring and isomorphic ring :) » 2009-12-23 09:37:45
1) Hint: All the ideals of are principal.
2) Hint: Does
have a multiplicative identity?#255 Re: Help Me ! » Homomorphis ring *** » 2009-12-23 09:26:34
Whats the problem?
#256 Re: Help Me ! » Normalize » 2009-12-02 03:50:01
Im getting a picture of probability density function in quantum mechanics here.
#257 Re: Puzzles and Games » A test problem... » 2009-11-13 00:28:41
To generalize:
Suppose there are teachers and given , we want that any or more teachers know all the answers but no or fewer teachers will know all the answers. Then the minimum number of questions is and each teacher is given answers.
#258 Re: Puzzles and Games » A test problem... » 2009-11-12 22:40:38
If S and T are two sets of four teachers and Q_S = Q_T then we must have S = T since S is the set of teachers who don't have the answer to Q_S and T is the set of teachers who don't have the answer to Q_T. Therefore we must have at least as many questions are there are sets of four teachers.
It took me a while but I finally understood it all.

To elaborate, the condition that no four (or fewer) teachers know all the answers means that if
are four teachers, there is an answer such that none of dont have . Now, suppose that are are distinct sets of four teachers such that there is an answer such that dont have and dont have the same answer . Since the sets of four are distinct, there is some such that . But if dont have , then the other six teachers must have (since every answer must be given to (at least) six teachers) and is one of these six teachers! Contradiction! Therefore, given distinct sets of four teachers, there must be distinct answers which they dont have. Hence the total number of answers must be at least the total number of selections of four teachers, i.e. .Thanks Avon! ![]() Youre a genius.
Youre a genius. 
#259 Re: Help Me ! » Battlefield problem » 2009-11-11 04:37:49
Your image file cant be found but I found the same post by you on another forum; this is Christopher Heckmans ASCII recreation of your diagram on www.mathkb.com.
+--+--+--+--+--+
| | | |x1| |
+--+--+--+--+--+
| | | |x2| O|
+--+--+--+--+--+
| |x3| | | |
+--+--+--+--+--+
| | | | | |
+--+--+--+--+--+
|x4| | |x5| |
+--+--+--+--+--+My gut feeling is that it cant be done but unfortunately I dont have a proof.
#260 Re: Puzzles and Games » A test problem... » 2009-11-11 04:32:39
Well, unless I see a counterexample, I will stick to 210 as the answer.
#261 Re: Puzzles and Games » Sudoku for kids - which starting age » 2009-11-10 23:43:36
I was thinking "level 3 of Cubilius" is Impossible I think there's a flaw in that game!
NO THERE ISNT!!

#262 Re: Puzzles and Games » A test problem... » 2009-11-10 20:32:28
Here is a smaller example to illustrate my point.
Suppose there are only 5 teachers, and we want that every combination of three or more teachers will have the complete set of answers but no combination or two or fewer teachers will. In this case each answer must be given to at least 3 teachers (otherwise there would be three teachers who dont have the complete set). Assume then that each answer is given to exactly 3 teachers. And now, if there are questions, we can arrange things so that given any two teachers, there will be exactly one question which is not given to them, as follows.
Teacher 1: {1,2,3,4,5,6}
Teacher 2: {1,2,3,7,8,9}
Teacher 3: {1,4,5,7,8,10}
Teacher 4: {2,4,6,7,9,10}
Teacher 5: {3,5,6,8,9,10}
Thus no two teachers have the complete set but any three teachers do. Again 10 may not be the minimum answer, but, as you can see for yourself, it works.
#263 Re: Puzzles and Games » A test problem... » 2009-11-10 20:14:28
Well, I can only say that the answer must be less than or equal to 210. This is my proof.
The first thing to note is that each answer must be given to at least 6 teachers otherwise there would be 5 teachers who wouldnt have one particular answer and this combination of five teachers wouldnt have the complete set of answers. And since we want that no four teachers have the complete set, we may as well assume that each answer is given to exactly 6 teachers.
Thus, if there are
questions, we can arrange things so that given any four teachers, there will be (exactly) one answer which is not given to these four and so they will not have the complete set. On the other hand any five teachers will have the complete set. If not, it would mean that one answer has not been given to these five teachers but we have already given every answer to six teachers so this cannot arise.If 210 is the answer, then each teacher will have
questions. However I cant prove that 210 is actually the minimum number; all Ive proved is that 210 works.#264 Re: Help Me ! » differential equations » 2009-11-10 08:27:07
xy'-y=0 (or, if you prefer: x(dx/dy)-y=0)
Doesnt actually mean ?
The way I do it is to solve the differential equation (by separating the variables and integrating) getting the general solution
. Hence the solution family is the set of all nonvertical straight lines through the origin, so is the common point you are looking for.#265 Re: Help Me ! » Groups » 2009-11-10 07:58:27
Consider the list
. Each is an even permutation, being a product of two odd permutations. They are also distinct, for by the cancellation law we have . Hence there are at least even permutations.Conversely, if
is an even permutation, then is an odd permutation and so is one of the permutations . Hence is one of the permutations .From this, we conclude that there are exactly
even permutations, i.e. there are as many odd permutations as even ones.#266 Re: Maths Is Fun - Suggestions and Comments » Intermediate Value Theorem » 2009-11-05 05:31:47
Or your route could be like this:
[align=center]http://www.mathsisfun.com/graph/functio … =-2&ymax=2[/align]
In which case the IVT applies but Rolles theorem does not!
#267 Re: Maths Is Fun - Suggestions and Comments » Intermediate Value Theorem » 2009-11-05 05:13:10
Rolles theorem requires the curve to be differentiable (i.e. smooth) not just continuous. MathsIsFuns example is about continuous routes, not smooth ones. You could e.g. walk up the side of a pyramid to the apex and down the another side in which case no part of your route is horizontal.
#268 Re: Dark Discussions at Cafe Infinity » Yes, it's true, I've solved it. » 2009-11-04 08:04:20
This is a very important result indeed. ![]() As Bertrand Russell and Alfred North Whitehead showed in their magnum opus Principia Mathematica, it is necessary to prove that 1 + 1 = 2 in order to re-invent mathematics with set theory.
As Bertrand Russell and Alfred North Whitehead showed in their magnum opus Principia Mathematica, it is necessary to prove that 1 + 1 = 2 in order to re-invent mathematics with set theory.
[align=center]http://www.youtube.com/watch?v=BE657F9sqyQ[/align]
#269 Re: Help Me ! » Simulations » 2009-11-01 21:56:41
And
#270 Re: Puzzles and Games » Five In A Line » 2009-10-30 11:21:13
I also thrashed the computer at Othello! Look!
[align=center]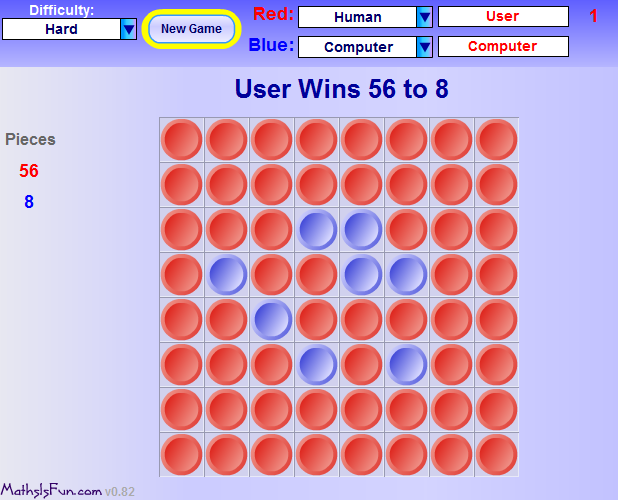 [/align]
[/align]
HAHAHAHAHA!!!!
#271 Puzzles and Games » Five In A Line » 2009-10-29 02:34:46
- JaneFairfax
- Replies: 4
Ive just played Five In A Line and given the computer a jolly good thrashing! Not only did I get five in a line, I actually got a six in a line and an additional five in a line!
[align=center]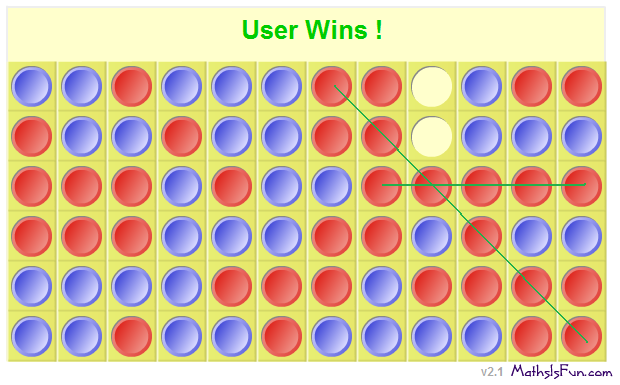 [/align]
[/align]
HAHAHAHAHA!!!!
#272 Re: Puzzles and Games » Eleven » 2009-10-26 02:30:00
Thanks! Fixed. ![]()
The point is that if your number is an odd multiple of 5, step 3 will produce a number ending in 24, while if your original number is a multiple of 10, step 3 will produce a number ending in 99. I forgot about the latter.
#273 Puzzles and Games » Eleven » 2009-10-25 23:08:13
- JaneFairfax
- Replies: 2
This is the latest number game invented by yours truly.
(1) Think of an integer and square it.
(2) Multiply together the number before and the number after the resulting square.
(3) If the last digit of the new number is 4 or 9, add 3; if the last digit is not 4 or 9, add 2.
(4) Multiply by 20 and subtract 29.
And the last two digits of the final number will always be!
#274 Re: This is Cool » Interesting pattern » 2009-10-25 01:11:55
Hence, if n is the number of 1s,
Now
Thus
Hence we have the required formula
[align=center]
[/align]#275 This is Cool » Interesting pattern » 2009-10-25 00:36:05
- JaneFairfax
- Replies: 4