Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#1 Re: Help Me ! » David Halber III.4 axiom » Yesterday 23:11:24
Axioms are the starting statements for any mathematical model. They are assumed to be true. From them, other statements can be proved. These are called theorems.
Angle BAC is defined as made by the rays AB and AC.
If A' and B' are two new points then the next axiom says that there is only one point C' so that angle ABC = angle A'B'C'.
It may not seem much at an early stage, but later in the development of theorems it may be important that C' is unique. This axiom also introduces that idea that two angles may be equal.
Bob
#2 Re: Help Me ! » English translation of Apollonius’s Conics » Yesterday 22:53:32
Thanks for the reply.
Can you see this image?
And what about this?
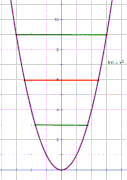
The first looks small and a bit blurred for me.
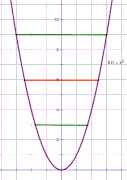
The second is larger and much sharper.
Both have the img /img format.
I'll repeat what I said in post 4. The y axis is the line of symmetry. The red and green lines are at 90 degrees to the axis and are bisected by it.
Bob
#3 Re: Help Me ! » English translation of Apollonius’s Conics » 2026-01-21 20:51:50
But you haven't answered any of my questions.
I'm at the limit of the help I can offer.
Try here:
https://www.mathsisfun.com/geometry/conic-sections.html
Bob
#4 Re: Help Me ! » English translation of Apollonius’s Conics » 2026-01-20 23:39:09
I'm so sorry this is proving so hard for you. My new image site offers the following possibilities. I'll number them so you can say which works for you.
(1) https://postimg.cc/4KJ9rhFk
(2) https://i.postimg.cc/bvn9SxxJ/symmetry_on_parabola.gif
(3) [symmetry_on_parabola.gif](https://postimg.cc/4KJ9rhFk)
(5) <a href="https://postimg.cc/4KJ9rhFk" target="_blank"><img src="https://i.postimg.cc/4KJ9rhFk/symmetry_on_parabola.gif" alt="symmetry_on_parabola"></a>
(7) <a href="https://postimages.org/" target="_blank"><img src="https://i.postimg.cc/bvn9SxxJ/symmetry_on_parabola.gif" alt="symmetry_on_parabola"></a>
(4) is the one they says should work for forums. That's what used when I changed post 4.
If none then what?
What device are you using? Does your own image show ok?
Maybe Phrontister will have some ideas for you. He has been a great help in sorting out the image problem for me.
Bob
#5 Re: Help Me ! » English translation of Apollonius’s Conics » 2026-01-20 06:11:34
Sorry. There's an internet 'war' going on between The UK government and Imgur so it has become more difficult to add images. Phrontister has found out how and my image should now be showing in post 4. But I'll add the image again here. Let me know is it now shows.

Bob
#6 Re: Help Me ! » English translation of Apollonius’s Conics » 2026-01-19 20:52:13
Many thanks Phro,
I knew you had said that before but I was in a hurry to get the picture up. I've corrected it now.
I can access Imgur if I I use a VPN. I've chosen Australia ![]() for this purpose.
for this purpose.
The UK's Ofgov site has a checking device, according to which the forum is not subject to the new law. So I've kept a copy of their statement about this and I'll just carry on for now and hope the police don't come knocking.
Bob
#7 Re: Help Me ! » English translation of Apollonius’s Conics » 2026-01-19 01:33:18
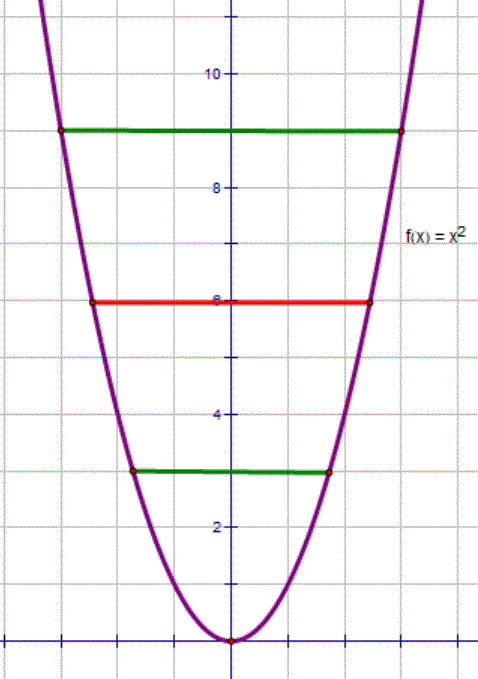
Success with posting image:

This shows a parabola f(x) = x² with the y axis as the line of symmetry. This is the axis your book is referring to.
The red and green lines are at 90 degrees to this axis and, as the axis is a line of symmetry, each is bisected by the axis.
You can try the same with the other curves. Circle is easy. You'll need a good equation plotter for the ellipse and hyperbola. There is one here:
https://www.mathsisfun.com/data/grapher-equation.html
Hope that helps.
Bob
#8 Re: Maths Is Fun - Suggestions and Comments » Enter your messaging details » 2026-01-18 07:26:31
hi,
I've read and re-read your post and I don't understand what you mean. Pretend I'm an 'old man' who isn't familiar with social media and spell it out in simple terms. I should add that, although I have administrator status, I don't have access to the underlying code for the forum, so I probably cannot make the change you are seeking anyway.
Best wishes,
Bob
#9 Re: Help Me ! » English translation of Apollonius’s Conics » 2026-01-18 07:20:24
Yes, I understand your confusion. The language is English but it's not how a modern English person would put it.
I used Google AI to get to the modern meaning. As it's a topic I am familiar with, I'll re-phrase myself.
The diagram shows a set of conic sections: a circle, an ellipse, a parabola, and (part of) a hyperbola. All these geometric shapes have a line of symmetry, usually called the axis. (The circle has many and the ellipse has two.)
Chords drawn across the axis at right angles to the axis are always bisected (cut in half) by the axis.
Hope that helps.
Bob
#10 Re: Help Me ! » Is it possible to write a formula for this graph? » 2025-12-25 21:55:51
hi criticalCat
Both answers correct.
The first and last functions are invertable, so you could construct a similar function definition for
x in terms of f(x). The middle has no inverse because many values of x lead to the same f(x); so there is no one formula that gives x when you know f(x).
Bob
#11 Re: Help Me ! » Is it possible to write a formula for this graph? » 2025-12-21 22:10:24
hi criticalCat
Weclome to the forum.
As the graph has three entirely different sections, it won't be possible to find a single formula for this. The usual way to describe a graph like this is by a piecewise definition.
ie. Find separate formulas for each section.
The first would be:
For x ≤ -4 f(x) = 3x + 25
Are you able to find the correct formulas for the other two sections?
Please post back.
Bob
#12 Re: Exercises » Bitter areas. » 2025-12-13 20:47:08
hi Phro, Thanks for the info. I was totallly unaware of this. I've followed the news about the UK Government's Online Safety legislation; I hadn't picked up on this side effect.
I've checked all my posts and I'm blocked from viewing every Imgur image! There's loads of them. I have copies on my computer but I haven't got the time or enthusiasm to switch them all. If asked by a poster I'll attempt to find my copy and get it on the site.
I haven't had a chance to check yet, but as I read it, I won't be able to log in to Imgur either.
What site are you now using?
And how long before that bans the UK too.
I'll give VPN a try when I get a moment.
Bob
ps. This could destroy us once the regulator gets to hear about us. ![]()
#13 Re: Exercises » Bitter areas. » 2025-12-11 01:11:44
hi Phro,
I'm getting a 'Content Not Viewable In Your Region' message instead of your Imgur images. Any idea why that is happening?
I've checked back on all your posts and old posts back to June '24 are also producing this message.
Bob
#14 Re: Help Me ! » division over 1/7 » 2025-12-10 00:26:52
hi Phrzby Phil
In that case, there's more. ![]()
A fraction either terminates or it recurs. A decimal that terminates can be shown to be a fraction, and the above shows that a recurring one can too.
So the set of all fractions (the rationals) is also the set of all terminating or recurring decimals.
So what else could there be?
Well it's fairly easy to construct a decimal that neither terminates nor recurs.
eg. 0.10010001000010000010000001..................... I'm adding an extra zero in each group of zeros before another 1.
It's possible to show that pi neither terminates nor recurs. I was shown the proof at University but I didn't really follow it then and I don't know how now.
e and the golden ratio are also such numbers. They are called the irrationals. Between every two rationals you can construct another; and also an irrational.
Between every two irrationals you can construct another and also a rational. So there are an infinite number of rational and irrationals.
But Cantor showed that the infinity of irrationals is bigger than the infinity of rationals. Whoops; that's a bit weird isn't it. But I do know his proof if you're interested. ![]()
Bob
#15 Re: Help Me ! » division over 1/7 » 2025-12-08 06:44:31
Every recurring decimal can be represented by a fraction. I'll show how by doing an example:
Firstly you need to separate any decimal figures that are not part of the recurring part. Those are easily dealt with separately.
Then you can use a 'sum to infinity' trick on the recurring part.
Finally combine the two parts to make the final fraction.
eg. 0.741212121212......
Split into 0.74 and 0.001212121212.....
0.74 is 74/100 so that's easily sorted.
let a/b - 0.00121212121212.......... (1)
As there are 2 recurring digits multiply this by 100. (n recurring digits multiply by 10^n)
100a/b = 0.1212121212121212..... (2)
Subtract (1) from (2). This removes the recurring bit completely.
99a/b = 0.12 Convert this to an integer only equation.
9900a/b = 12
This means that a/b = 12/9900
Now recombine the two fractions:
74/100 + 12/9900 = ( 7326 + 12 )/9900 = 7338/9900
Bob
#16 Re: Help Me ! » Problem of permutation and combination » 2025-10-03 20:30:55
OK I've got it.
If one grade gets 3, then there are 3 ways to achieve this so 3 x 5!. But some possibilities are repeated. I am counting vwx, vxw, wvx, wxv, xvw, xwv so I need to divide by 6.
If 2 grades get 2 each, again 3 ways, so 3 x 5!, but this time I'm counting vy and yv in one grade and wz and zw in a second grade so I need to divide by 2! and 2! again.
So I should have calculated thus:
Bob
#17 Re: Help Me ! » Problem of permutation and combination » 2025-10-03 20:10:50
Oh whoops! ![]()
I thought my answer was correct so I was looking for a way to show this. I started with the second part of Luiz's anaswer and showed 90 was correct. So then I tackled the first part and made that careless error. Very sorry.
The good news is I seem to have shown by 'exhaustion' that 150 is correct.
Bad news. I cannot see what is wrong with my analysis either. So I'm back to the 'drawing board' to find why.
Apologises for my excessive use of English metaphors.
Bob
#18 Re: Help Me ! » Problem of permutation and combination » 2025-10-03 01:41:15
I only get 30 for that first group
Calling the equipment types V W X Y Z and giving three to 1st grade we have
VWX Y Z
VWX Z Y
____________________
VWY X Z
VWY Z X
____________________
VWZ X Y
VWZ Y X
____________________
____________________
VXY W Z
VXY Z W
____________________
VXZ W Y
VXZ Y W
____________________
____________________
VYZ W X
VYZ X W
____________________
____________________
WXY V Z
WXY Z V
____________________
WXZ Z Y
WXZ Y Z
WYZ V X
WYZ X V
____________________
XYZ V W
XYZ W V
____________________
That makes 10 ways. Then multiply by 3 for 2nd and 3rd grades getting the three. 30 + 90 = 120
Bob
#19 Re: Help Me ! » Analytic continuation(simple?) » 2025-10-02 21:56:46
ho hypsin_0
Apologies that I have not posted sooner. I was away from home trying to use a poor (hotel) wifi. So I had an idea on paper but couldn't post it.
f(1)=2
f(z+1)=2^f(z)
First I'll try positive z.
f(2) = f(1+1) = 2^2 = 4
f(3) = f(1+2) = 2^4= 16
f(4) = f(1+3) = 2^16 = 65536
.......
Is there a single formula for this?
No one seems to have found one that is not iterative.
Google ai says this is called tetration and only gives an iterative formula. Wolfram Alpha says the same.
So what about zero and negative z?
f(1) = f(1+0) = 2^[f(0)] But we know this is 2 so this implies f(0) = 1
f(0) = f(1 + (-1) ) = 2^ f(-1) But we know this is 1 so this implies f(-1) = 0
f(-1) = f(1 + (-2) ) = 2^f(-2) But we know this is 0 so we need a power of 2 that makes 0. No such exists so f(-2) is undefined and also f(z) where z is lower that -2.
That's all I've got.
Bob
#20 Re: Maths Is Fun - Suggestions and Comments » Math Entry Test » 2025-10-02 21:29:59
Oh. Don't know why that is.
I have emailed MIF and I am awaiting a reply.
Bob
#21 Re: Help Me ! » Problem of permutation and combination » 2025-10-02 21:25:20
hi Luiz,
I'll have a go.
Firstly I'll ignore what kind of equipment is allocated and just work out the ways of distributing identical equipment
Every grade must have one, so I just need to consider what to do with the remaining two.
I think there are 6 options:
Ist grades get both; 2nd grades get both; 3rd grades get both;
Ist and 2nd get one each; 1st and 3rd get one each; 2nd and 3rd get one each.
Now to consider the different types of equipment. I can shuffle what is allocated in 5! ways.
So I think the answer to your question is 6 times 5! = 720 ways.
Bob
#22 Re: Maths Is Fun - Suggestions and Comments » Math Entry Test » 2025-09-29 00:24:42
Oh, I thought you had cracked it. Longer standing Members with existing avatars continue to have them after the upgrade. More recent members find nothing happens when they follow the instructions.
Bob
#23 Re: Maths Is Fun - Suggestions and Comments » Math Entry Test » 2025-09-29 00:19:16
hi Ganesh,
No cause for concern. ktesla39 and I have been trying to find a way to protect the forum from spammers. He has made a copy that he can experiment with without any threat to MIF. Note. He has already found a way to create an Avatar.
I've updated MIF about this.
Bob
#24 Re: Maths Is Fun - Suggestions and Comments » Math Entry Test » 2025-09-28 02:52:34
Test post.
https://www.google.com/
https://www.mathsisfun.com/data/function-grapher.html
https://www.bbc.co.uk/
math
math
https://www.google.com/ https://www.mathsisfun.com/data/function-grapher.html https://www.bbc.co.uk/
https://www.google.com/https://www.mathsisfun.com/data/function-grapher.htmlhttps://www.bbc.co.uk/
I can stop multiple posting if the hyperlinks are all on one line but not if there's a newline between them. ![]()
Actually I cannot stop them even then as the last two show.
Bob
#25 Re: Maths Is Fun - Suggestions and Comments » Math Entry Test » 2025-09-26 04:37:35
Every day I have to remove members who only joined so they can advertise on our site. It's a lot harder to do if the person uses a guest post rather than a member post so I have configued the guest group so they cannot do this. Sad but necessary or we'd become overwhelmed by rubbish, much of it downright offensive.
It would be wonderful if there was a mechanism that imposed some sort of post restriction on new members, but, as far as I can think, the only way for a new member to qualify would be to make posts, so I'm in a Catch 22 here. Suggestions welcome.
Bob