Posts by ben

ben · Euler Avenue

Recall that, given

as a linear operator on vector spaces, we found as the linear operator that maps onto , and called it the push-forward of . In fact let's make that a definition: defines the push-forward.

This construction arose because we were treating the space

as a fixed domain. We are, of course, free to treat as as fixed codomain, like this.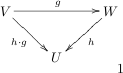

This seems to make sense, certainly domains and codomains come into register correctly, and we easily see that .

Using our earlier result, we might try to write the operator

, but something looks wrong; is going "backwards"!

Nothing daunted, let's adopt the convention

. (We will see this choice is no accident)

Looking up at my diagram, I can picture this a pulling the "tail" of the h-arrow back along the g-arrow onto the composite arrow, and accordingly (using the same linguistic laxity as before), call

the pull-back of , and make the definition: defines the pullback

(Compare with the pushforward)

This looks weird, right? But it all makes beautiful sense when we consider the following special case of the above.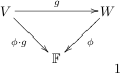

where I have assumed that

is the base field for the vector spaces . As before, the composition makes sense, and I now have , and the pullback . But, hey, lookee here....

is the vector space of all linear maps - functionals - , so we quite simply have that , the dual vector spaces.

Putting this all together I find that, for

I will have as my pullback.

I say this is just about as nice as it possibly could be. What say you?

ben · Euler Avenue

This is so much fun! Look

We will suppose that

are vector spaces, and that the linear operators (aka transformations) . Then we know that the composition as shown here.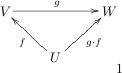

Notice the rudimentary (but critical) fact, that this only makes sense because the codomain of

is the domain of

Now, it is a classical result from operator theory that the set of all operators

is a vector space (you can take my word for it, or try to argue it for yourself).

Let's call the vector space of all such operators

etc. Then I will have that are vectors in these spaces.

The question naturally arises: what are the linear operators that act on these spaces? Specifically, what is the operator that maps

onto ?

By noticing that here the

is a fixed domain, and that , we may suggest the notation . But, for reasons which I hope to make clear, I will use a perfectly standard alternative notation .

Now, looking up at my diagram, I can think of this as "pushing" the tip of the f-arrow along the g-arrow to become the composite arrow. Accordingly, I will call this the push-forward of

on , or, by a horrid abuse of English as we normally understand it, the push-forward of

So, no real shocks here, right? Ah, just wait, the fun is yet to begin, but this post is already over-long, so I'll leave you to digest this for a while.........

ben · Euler Avenue

Ricky wrote:

Prove that card(A) < card(P(A)), where card(A) is the cardinality of A, and P(A) is the power set of A.

Yes, your proof is good, I think, but Cantor's own proof was a lot sweeter, if you'll forgive me for saying so. Plus it requires (almost) no knowledge of mathematics!

You do know it, don't you? If not, and if anyone wants, I'll try and dredge it up from the memory bank.

ben · This is Cool

darn, then I'm nearly (not quite) as wrong as old Poincaré. Ah well (interesting software, by the way - my d-a-m-n was changed to darn. How sweet!)

ben · This is Cool

Ricky wrote:

I Fully Understand the Problem!
I strongly doubt that.

I don't "strongly doubt it", I know it

People don't understand what a manifold is or what it means to be homeomorphic.

Careful here! {ben} is a singleton in the powerset {P(people)}

ben · This is Cool

The fact that I have taken the Apple and the Doughnut as the Problem example! is no more foolish or Stupid than the original Statement below to Describe the Problem using of all things Rubber Bands?? (Thats also not Math? )

But you seem not to understand that what you you call "apples" (2-sphere) and "doughnuts" (2-torus) are classic examples of 2-manifolds. The P. conjecture is relatively easy to prove in the 2-dimensional case, exceptionally difficult for the 3-manifold case. Hence the prize. Ricky has it right; this is the Poincaré conjecture:

Ricky wrote:

Every simply connected closed three-manifold is homeomorphic to the three-sphere.

So, before you start spouting off your nonsense, make sure that (at the very least) you understand what a manifold is, what it means for it to be connected and what the word homeomorphic means. Until you have that under your belt, you are not qualified to comment.

ben · Euler Avenue

Ricky wrote:

You know you were projecting when you said, "Surely you don't need me to show you, do you?", and you know it.

I might if I knew what "projecting" means. Obviously, by your tone, it's a negative thing, but in fact, my comment was intended as flattery - as in, of course you know Cantor's thm.

Anyway, you got me thinking. Ricky, I know you don't need this little tutorial, but here goes, for general consumption.

There is a load of laxity in language regarding "infinity". Consider the subset A = [a, b] of R. By the definition of [ , ], no element of A is infinite. But by the definition of R (well, it's not really a definition, it's a continuity axiom), the cardinality of [a, b] is infinite and uncountably infinite to boot.

See what I mean about laxity?

ben · Euler Avenue

Ricky wrote:

Countably finite.

This is weird, Ricky. surely you're not suggesting the possible existence of an "uncountable finite" set?

Countable implies a bijection to the natural numbers, which in turn implies infinite.

No, this is wrong. Why do you think this? All finite sets are countable, almost by definition. It's true that a set is said to be countable if there is a bijection to a subset of N, and as N is "countably infinite" again by definition, and as N is always a subset of N, the bijection you refer to may or may not imply a set is countably infinite, it could easily be finite (we don't need the countably bit for finite sets). But it is most certainly not the case that countable implies infinite.

Oh yes, and leave off the "your perch" bit if you don't mind - I am tolerant, but not infinitely so

ben · Euler Avenue

Laterally Speaking wrote:

Basically, that number is pretty much infinite, being that time can be divided into infinitely small units.

Well, well, I see you guys are still tying yourselves in knots. What is "pretty much infinite"? Like 0.999... is "pretty much" 1? Oh dear, oh dear. And...

Ricky wrote:

If the universe is continuous then there are an infinite amount of states. If it is discrete, then it's still just about impossible to calculate

Think on Cantor's theorem, Ricky. If what you're all calling the "universe" is discrete, then it is countable. If it's not discrete, then it's not countable, by Cantor's thm. Surely you don't need me to show you, do you?

ben · Euler Avenue

Laterally Speaking wrote:

I feel like Euler Avenue is a deserted wasteland... nobody's posted for almost a month here.

Then the solution is simple - start an interesting and challenging thread of your own. I can offer a host of these, if you want.....

Or are you just a consumer, rather than a producer?

ben · Euler Avenue

So, lemme see if I can make the inner product easier.

First recall the vector equation I wrote down:

. I hope nobody needs reminding this is just shorthand for . The scalars are called the components of v. Note that the do not enter explicitly into the sum; they merely tell us in what direction we want to evaluate our components. (v is a vector, after all!).

So we can think of our vector projecting

units on the ith axis. But we can ask the same question of two vectors: what is the "shadow" that, say, v casts on w? Obviously this is at a maximum when v and w are parallel, and at a minimum when they are perpendicular (remember this, it will become important soon enough.

OK, so in the equation I wrote for the inner product

what's going on? specifically, why did I switch indices on b, and what happened to the coordinates, the x's?

Well, it makes no sense to ask, in effect, what is v's projection in the x direction on w's projection on the y axis. So we only use like pairs of coordinates and components, in which case we don't need to write down coordinates. In fact it's better if we don't, since we want to emphasize the fact that the inner product is by definition scalar. This what the Kroenecker delta did for us. It is the exact mathematical equivalent of setting all the diagonal entries of a square matrix to 1, and all off-diagonal entries to 0!

On last thing. Zhylliolom wrote the inner product as something a bit like this <v,w>. I prefer (v, w), a symbol reserved in general for an ordered pair. There is a very good reason for this preference of mine, which we will come to in due course. But as always, I've rambled on too long!

ben · Euler Avenue

Zhylliolom wrote:

Just a concern; when you say that
you are assuming an orthonormal basis in cartesian coordinates

You're right, I am, I was kinda glossing over that at this stage. Maybe it was confusing? You are jumping a little ahead when you equate good ol' v · w with (v,w), but yes, I was getting to that (it's a purely notation convention). But I really don't think, in the present context, you should have both raised and lowered indices on the Kroenecker delta; I don't think that

makes any sense (but see below).

This is certainly fine in an introduction, as the inner product is given as

Ah, well, again you are jumping ahead of me! your notation

usually refers to the product of the components of a dual vector with its corresponding vector, as I'm sure you know. I was coming to the dual space, in due course.

Overall I just feel that the inner product section is a bit shaky. For example, you never tell the reader that
even though you substitute it into your formula out of nowhere.

Well, I never did claim that equality, both my indices were lowered, which I think is the correct way to express it (I can explain in tensor language if you insist). But, yeah, OK, let's tidy it up, one or the other of us, but if you do want to have a pop (feel free!) make sure we are both using the same notation

ben · Euler Avenue

So, it seems there are no problems your end. Good, where was I? Ah yes, but first this: I said that a vector space comprises the set V of objects v, w together with a scalar field F and is correctly written as V(F). Everybody, but everybody abuses the notation and writes V for the vector space; we shall do this here, OK with you?

Good. We have a vector v in some vector space V which we wrote as

, where the are scalar and the are coordinates.

We also agreed that, when using Cartesian coordinates (or some abstract n-dimensional extension of them) we require them to be mutually perpendicular. Specifically we want the " projection" of each

on each (i ≠ j) to be zero. We'll see what we really mean by this in a minute.

So now, I'm afraid we need a coupla definitions.

The inner product (or scalar product, or dot product) of v, w ∈ V is often written v · w = a (a scalar). So what is meant by v · w? Let's see this, in longhand;

let

and . Then .

Now this looks highly scary, right? So let me introduce you to a guy who will be a good friend in what follows, the Kroenecker delta. This is defined as

if i = j, otherwise = 0.

So we find that

So, to summarise,

. Now can you see why it's sometimes called the scalar product? Any volunteers?

Phew, I'm whacked, typesetting here is such hard work!

Any questions yet?

ben · Euler Avenue

Sorry for the delay in proceeding, folks, I had a slight formatting problem for which I I have found a partial fix - hope you can live with it. But first this;

When chatting to jane, I mentioned that the real line R is a vector space, and that we can regard some element -5 as a vector with magnitude +5 in the -ve direction. But of course there is an infinity of vector in R with magnitude +5 in the -ve direction. I should have pointed out that, in any vector space, vectors with the same magnitude and direction are regarded as equivalent, regardless of their limit points (they in fact form an equivalence class, which we can talk about, but it's not really relevant here)

We agreed that a vector in the {x,y} plane can be written

, where are scalar. We can extend this to as many Cartesian dimensions as we choose. Let's write , i = 1,2,...,n. (note that the superscripts here are not powers, they are simply labels.

Now, you may be thinking I've taken leave of my senses - how can we have more that 3 Cartesian coordinates? Ah, wait and see. But first this. You may find the equation

a bit daunting, but it's not really. Suppose n = 3. All it says is that there is an object called v whose direction and magnitude can be expressed by adding up all the units (the ) that v projects on the coordinates . Or, if you prefer, v has projection along the th coordinate.

Now it is a definition of Cartesian coordinates that they are to be perpendicular, right? Then, to return to more familiar territory, the x-axis has zero projection of the y-axis, likewise all the other pairs. This suggests that I can write these axes in vector form, so take the x-axis as an example. x = ax + 0y + 0z, this is the definition of perpendicularity (is this a word?) we will use. So, hands up - what's "a"? Yeah, well this alerts us to a problem, which I'll state briefly before quitting for today.

You all said "I know, a = 1" right? But an axis, by definition, extends to infinity, or at least it does if we so choose. So, think on this; an element of a Cartesian coordinate system can be expressed in vector form, but not with any real sense of meaning. The reason is obvious, of course: Cartesian (or any other) coordinates are not "real", in the sense that they are just artificial constructions, they don't really exist, but we have done enough to see a way way around this.

More later, if you want.

ben · Maths Is Fun - Suggestions and Comments

Is there some trick I'm missing to get LaTex to format in-line, preferably with a smaller font. I've tried every trick I know, without sucess.

Just for example, what I'm objecting to is something like this:

The sum over over all basis vectors

with components is , i = 1, 2, ...,n.

Check my raw text to see that what appears is not what I intended.

ben · Euler Avenue

Ricky: Yes, I was going to touch on polynomial space in a bit, I wanted to get established first, however, I think I may have to address this first;

Jane: I don't at all like the way you expressed this, so I guess I'll have to take a bit of a detour.

Consider R, the real numbers. We grew up with them and their familiar properties, and some of us became quite adapt at manipulating them in the usual ways. But we never stopped to think of what we really meant by R, and what the properties really represent. Abstract algebra, which is what we are doing here, tries to tease apart those particular properties that R shares with other mathematical entities.

It turns out that R is a ring, is a field, is a group, is a vector space, is a topological space......., but there are groups that are not fields, vector spaces that are not groups and so on. So it pays to be careful when talking about R, by which I mean one should specify whether one is thinking of R as a field or as a vector space.

So, what you claim is not true, in the sense that the field R is a field, not a vector space. What is true, however, is that R, Q, C etc have the properties of both fields and vector spaces. So for example, if I say that -5 is a vector in R, I mean there is an object in R that has magnitude +5 in the -ve direction. Multiplication should be thought of as applying a directionless scalar, say 2, which is an object in R viewed as a scalar field.

I hope this is clear. Sorry to ramble on, but it's an important lesson - R, C and Q are dangerous beasts to use as examples of, well anything, really, because they are at best atypical, and at worst very confusing.

ben · Euler Avenue

A vector is a mathematical object with both magnitude and direction. This much should be familiar to you all. Consider the Cartesian plane, with coordinates x and y. Then any vector here can be specified by v = ax + by, where a and b are just numbers that tell us the projection of v on the x and y axes respectively.

Now it is natural in this example to think of v as being an arrow, or "directed line segment" to give it its proper name. But as the dimension of the containing space increases, this becomes an unimaginable notion. And in any case, for most purposes this is a far too restricted idea, as I will show you later.

So, I'm going to give an abstract formulation that will include the arrows in a plane, but will also accommodate more exotic vectors. So, here's a

Definition. A vector space V(F) is a set V of abstract objects called vectors, together with an associated scalar field F such that:

V(F) forms an abelian group;
for all v in V(F), all a in F, there is another vector w = av in V(F);
for any a, b in F, and v, w in V(F) the following axioms hold;
a(bv) = (ab)v;
1v = v;
a(v + w) = av + aw;
(a + b)v = av + bv.

Now I've used a coupla terms you may not be familiar with. Don't worry about the abelian group bit - probably you'd be appalled by the notion of a non-abelian group, just assume that here the usual rules of arithmetic apply.

About the field, again don't worry too much - just think of it as being a set of numbers, again with the usual rules of manipulation (there is a technical definition, of course). But I do want to say a bit about fields.

The field F associated to the set V ( one says the vector space V(F) is defined over F) may be real of complex. All the theorems in vector space theory are formulated under under the assumption that F is complex, for the following very good reason:

Suppose I write some complex number as z = a + bi, where i is defined by i² = -1. a is called the real part, and bi the imaginary part. When b = 0, z = a + 0i = a, and z is real. It follows that the reals are a subset of the complexes, therefore anything that is true for a complex field is of necessity true of a real field. However, there are notions attached to the manipulation of complex numbers (like conjugation, for example) which don't apply to real numbers, or rather are merely redundant, not wrong. Formulating theorems under the above assumption saves having two sets of theorems for real and complex spaces.

You will note, in the definition of a vector space above, that no mention is made of multiplication of vectors - how do yo multiply arrows? It turns out there is a sort of way, well two really, but that will have to wait for another day. Meantime, any questions, I'll be happy to answer.

ben · Euler Avenue

First, Zhylliolom: yes maybe I was being a bit of a prima donna, but it's so hard to know without some come-back. Maybe one of these days I'll resurrect the Lie Group thread. We'll see, but I take your point about your members here; there is also the worry that, if people log onto a site that declares math to be fun, and are faced with a barrage of mystifying stuff, they might conclude that math is no fun at all!

MathIsFun: Gimme a day or two to get a Vector Space thread together. I'm not sure I'm the right person to make a website page on it, but if I do start a thread you will all be free to make use of it for that purpose.

ben · Euler Avenue

Ricky wrote:

Rather, we use a probabilistic thing such as a wave function to set off a trigger.

Well actually, it's the absolute square of the wave function psi, which is itself an eigenfunction. For, wave functions have, by definition, codomain [-1,1], which makes no sense probabilistically.

Ha! I am tempted to start a thread on linear vector spaces, where all this might be explained. But, judging from the responses to my previous "lectures" I am not confident it would be well received.

Anybody have any thoughts (it is a cool subject, and only involves simple arithmetic)?

ben · Euler Avenue

Good point Ricky, I hadn't thought of that (but why would I?)

ben · Euler Avenue

JaneFairfax wrote:

Then I could add to the list in my first post:
3. Let x be a phenomenon (e.g. Schrödingers cat ) satisfying both conditions A and conditions B. Then x is both alive and dead!

OK Jane, nice post. Just for fun, note this. I am not a physicist, but was recently told that Schroedinger devised the "cat-in-a-box" thought experiment to illustrate what he regarded as the illogicality of quantum mechanics (or do I mean the Copenhagen interpretation? Not sure)

And now the cat in its box is in all the texts as a perfect illustration of how QM works. Poor old Schroedinger!

ben · Euler Avenue

JaneFairfax wrote:

I should point out at this stage that whole point of this thread is to take a light-hearted look at the way mathematical language is used in particular, at how certain mathematical terms differ in meaning from the way those terms are used in ordinary language. This thread is not meant to be a serious critique of mathetical language itself it is only a light-hearted comparison of mathematical and non-mathematical language.

In that case I apologize (I'm always the last to get a joke in a crowd).

You are right. In fact, when I first started in science, it really pissed me off at what I thought was the hijacking or "ordinary" words for technical purposes. I now see it as inevitable - as I said, ordinary usage is so imprecise as to be virtually useless.

Good, we agree.

ben · Euler Avenue

Ricky wrote:

I don't believe that Jane is talking about true contradictions. Rather metaphorical ones. We name mathematical things with metaphors.

As we do with any language, English, German or mathematics. We can get philosophical if you want - in fact there is a whole area of mathematics called category theory which straddles math and philosophy.

Let me just say this, though. It is my belief that mathematics defines terms with rather more precision that everyday language does: what is the connection between an open door, an open mind, an open judicial case etc.? It's hard to pin down without using a further metaphor. But in topology, the terms open and closed are very precisely defined, and they don't really conflict with ordinary usage.

I note that Jane uses the horrid word "clopen" to mean both open and closed. This has as its only virtue the fact that it doesn't collide with the common usage of open and closed.

But regarding zero, there is a problem. First there seems to be a confusion here between imaginary and complex numbers. An imaginary number is of the form bi, where i is defined as i² = -1. A complex number is defined as a + bi, for all real a and b. A real number is defined to be a subset of the complex numbers when b = 0, i.e. a = a + 0i.

Now it is in the nature of any set with identity (monoid, group, ring,.....) that it must share the identity with its subset. So that fact that R and C share the additive identity, 0, comes as no surprise, and is certainly not a contradiction metaphorical or otherwise. This would be like thinking of 3 as both real and prime as a contradiction!

ben · Euler Avenue

What is your point, Jane? Where are the terminological contradictions? I see none here.

Take a look at http://www.mathsisfun.com/forum/viewtopic.php?id=4134

ben · Euler Avenue

Sure, forgive me, it was Monday night = Grumpy night. Sorry for any offense.

Anyway, I guess I never really "left" this forum, just got bored with the content - my fault, not yours.... Ah well, as I say, it's me at fault. Take care, all.

-b-

Math Is Fun Forum

#1 Re: Euler Avenue » Push-me, pull you » 2009-04-03 09:22:08

#2 Euler Avenue » Push-me, pull you » 2009-04-02 07:25:10

#3 Re: Euler Avenue » Interesting proofs » 2007-08-01 07:50:46

#4 Re: This is Cool » THE POINCARE CONJECTURE PROOF - By Anthony.R.Brown 12/06/07 » 2007-06-15 04:44:07

#5 Re: This is Cool » THE POINCARE CONJECTURE PROOF - By Anthony.R.Brown 12/06/07 » 2007-06-15 04:27:43

#6 Re: This is Cool » THE POINCARE CONJECTURE PROOF - By Anthony.R.Brown 12/06/07 » 2007-06-14 05:35:39

#7 Re: Euler Avenue » Number Giants » 2007-06-13 03:58:49

#8 Re: Euler Avenue » Number Giants » 2007-06-12 10:35:36

#9 Re: Euler Avenue » Number Giants » 2007-06-12 04:51:18

#10 Re: Euler Avenue » Number Giants » 2007-06-06 06:48:24

#11 Re: Euler Avenue » Vector spaces. » 2007-04-18 02:06:10

#12 Re: Euler Avenue » Vector spaces. » 2007-04-17 08:23:11

#13 Re: Euler Avenue » Vector spaces. » 2007-04-17 06:40:38

#14 Re: Euler Avenue » Vector spaces. » 2007-04-16 04:04:13

#15 Re: Maths Is Fun - Suggestions and Comments » . » 2007-04-14 04:16:18

#16 Re: Euler Avenue » Vector spaces. » 2007-04-11 23:13:12

#17 Euler Avenue » Vector spaces. » 2007-04-11 02:08:54

#18 Re: Euler Avenue » Contradictory mathematical terminologies? » 2007-04-08 07:24:34

#19 Re: Euler Avenue » Contradictory mathematical terminologies? » 2007-04-07 06:11:29

#20 Re: Euler Avenue » Contradictory mathematical terminologies? » 2007-04-05 02:10:04

#21 Re: Euler Avenue » Contradictory mathematical terminologies? » 2007-04-03 07:40:59

#22 Re: Euler Avenue » Contradictory mathematical terminologies? » 2007-04-02 05:42:00

#23 Re: Euler Avenue » Contradictory mathematical terminologies? » 2007-04-02 03:14:51

#24 Re: Euler Avenue » Contradictory mathematical terminologies? » 2007-03-31 07:41:12

#25 Re: Euler Avenue » About this forum » 2007-03-27 07:11:42

Board footer