Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#1 Re: Exercises » Matrix chain multiplication question » 2013-04-29 07:11:25
Dimensions A2 x A3. Sorry.
#2 Exercises » Matrix chain multiplication question » 2013-04-28 05:05:49
- genericname
- Replies: 3
Let's say for example,
Matrices A1;A2;A3 with dimensions:
A1 = 5x10
A2 = 10x3
A3 = 3x10
Would M[2,3] be equal to (10*3*10) or (10*3)?
#3 Re: Exercises » Proof by induction question » 2013-03-19 03:16:51
Oh, I see. Thank you, bob.
#4 Re: Exercises » Proof by induction question » 2013-03-18 16:38:32
Multiplying out the bracket? Sorry, think I might be misunderstanding something, but wouldn't that be (9^(n-1)) - 3 + 2 if you multiply by 3?
#5 Re: Exercises » Proof by induction question » 2013-03-18 07:29:27
Oops, it was a typo. Sorry! It was supposed to be (3^n)-1 like what Bob said.
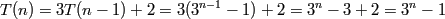
How did you get rid of the n-1 in that step?
#6 Exercises » Proof by induction question » 2013-03-18 06:26:40
- genericname
- Replies: 7
Hi, I am stuck on the last step. What am I supposed to do now?
Problem: Let T(n)=3T(n-1)+2, T(1)=2. Prove by induction that T(n)=3^(n-1)
Here is what I have so far:
Show base case k=1: T(1) = 3^1 - 1 = 2
Show for k=n-1: T(n-1) = (3^((n-1)-1)) -1
Show for k=n :
3((3^(n-2)) - 1) + 2
#7 Re: Help Me ! » Log question » 2013-02-26 03:44:16
Ah, thank you. It was base 2, sorry for the confusion.
#8 Re: Help Me ! » Log question » 2013-02-25 08:58:06
Yeah.
#9 Help Me ! » Log question » 2013-02-25 08:33:05
- genericname
- Replies: 9
(2*(n/2)*lg(n/2)) + n
= (n*lg(n/2))+n
= n*(lg n - 1) + n
How does (n*lg(n/2))+n simplify to n*(lg n - 1) + n? What happened to the n/2 that was inside? It has been a while since I last worked with log.
#10 Re: Exercises » Gamma function question » 2012-12-04 09:47:56
Sorry, I don't recall.
#11 Exercises » Gamma function question » 2012-12-04 05:35:38
- genericname
- Replies: 3
Hi, I'm confused about how to find the value of this specific problem. The answer is supposed to be (1/2) * sqrt(pi), but how?
If gamma(1/2) is = sqrt(pi), what is gamma(3/2)?
#12 Re: Help Me ! » What is the formula for finding Z in this case? » 2012-12-02 13:58:03
Oh! I see. As always, thanks! ![]()
#13 Re: Help Me ! » What is the formula for finding Z in this case? » 2012-12-02 10:41:20
Ah, the answers were mixed up. The answer is actually 1.96. How did they get that?
#14 Help Me ! » What is the formula for finding Z in this case? » 2012-12-02 07:50:36
- genericname
- Replies: 4
Hi, the problem is:
Find Z.025; that is find Z which cuts off a right-hand tail probability 0.025
The "Z.025" part looks like this:
http://i.imgur.com/CnZdc.png (didn't know how to type it out)
The answer is .70, but I don't know how it was calculated.
#15 Re: Exercises » Chebyshev's theorem problem » 2012-11-04 06:59:20
The next part of the problem wanted us to compare the answers to the predictions of Chebyshev's theorem.
#16 Re: Exercises » Chebyshev's theorem problem » 2012-11-04 06:49:45
The example for when k=2 said that you have to integrate f(x) from something to something to compute p( _ < X < _ ) so I assumed that I had to. It was listed as an Exponential distribution problem and it said to do the same with k= 3 and 4.
#17 Exercises » Chebyshev's theorem problem » 2012-11-04 05:21:41
- genericname
- Replies: 7
For the exponential density f(x) = 3e^-3x, compute the actual probability for k=3 and k=4.
Expected value = 1/3. The variance is 1/9 and the standard deviation is 1/3 so for k=3 I got:
(1/3) - 3*(1/3) < X < (1/3) + 3*(1/3) (Wasn't sure about this, all I did was sub 2 with 3 from the problem where k=2.)
= -2/3 < X < 4/3
So to get the probability, you integrate f(x) from -2/3 to 4/3? Would this be correct?
#18 Re: Exercises » Question about geometric series » 2012-10-30 07:16:16
Thank you, bob.
#19 Exercises » Question about geometric series » 2012-10-30 06:14:59
- genericname
- Replies: 2
Hi, how do I prove that the sum of all the probabilities is equal to 1 for this problem?
Flip a coin until heads show, assume that the probability of heads on one flip is 4/5. We define a random variable X = the number of flips.
a) What are the possible values of X?
b) Find the probability distribution for X: give the first four values and then find a general formula for the probability that X = n
c) Prove that the sum of all probabilities is 1 using the formula for the sum of a geometric series.
My answers:
a) X=1,2,3,...,n
b)
p(1) = 4/5
p(2) = 4/25
p(3) = 4/125
p(n) = ((1/5)^n-1) * (4/5)
#20 Re: Exercises » Random variable question » 2012-10-28 04:45:20
The course is Elementary Probability and Statistics.
#21 Re: Exercises » Random variable question » 2012-10-28 02:51:49
I think it means that something can be completely counted. Not quite sure.
#22 Exercises » Random variable question » 2012-10-27 16:19:35
- genericname
- Replies: 5
Hi, I am a bit confused about this problem.
For each of the following random variables, tell whether it would naturally represent a finite, discrete or continuous random variable. Explain your reasoning.
a) X is the number of customers who walk into a shop between noon and 1PM on some particular day.
b) X is the amount of orange juice in a randomly chosen 8-ounce carton of juice.
c) X is the amount of times you play the lottery until you win? We'll assume that once you win you stop playing.
d) X is the number of women in a randomly chosen sample of 500 New York City residents.
For the answers I got:
a) Finite because the amount of people between the noon and 1PM are countable.
b) Continuous because the amount of juice is uncountable.
c) Continuous because you don't know when you will win.
d) Discrete because it is taking a number of people from a set amount.
#23 Re: Exercises » Probability density question » 2012-10-20 12:13:31
Ah, thank you. I was overthinking it.
#24 Re: Exercises » Probability density question » 2012-10-20 11:51:38
How does it come up to 8/3? (Sorry for the dumb questions)
#25 Re: Exercises » Probability density question » 2012-10-20 11:42:39
I'm not quite understanding it. The value of x = 0, 1, 2, 3, 4?