Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#1 Re: Help Me ! » textbook on statistics » 2022-08-07 08:17:53
Mathegocart wrote:Hey 666 bro,
I'd recommend the book Statistical Inference(ISBN-13:978-0534243128) by George Casella and Roger L. Berger. Statistics is quite the varied field and there's not one generally accepted view on how to approach it. But the book Statistical Inference is comprehensive, robust, and remarkably understandable.thanks Mathegocart i'll have a look on that book.
You're welcome. Let me know how your journey in statistics goes.
#2 Re: Help Me ! » textbook on statistics » 2022-08-02 10:44:59
Hey 666 bro,
I'd recommend the book Statistical Inference(ISBN-13:978-0534243128) by George Casella and Roger L. Berger. Statistics is quite the varied field and there's no one generally accepted view on how to approach it. But the book Statistical Inference is comprehensive, robust, and remarkably understandable.
#3 Re: Introductions » Hi » 2022-07-29 20:08:49
Hello John(or AT&T as per your moniker),
Welcome aboard. And glad to see your interest in linguistics. And may I say that Lucien Tesnière appears to be quite the shrewd man with his foundational work on syntax. I've learned something new today. As for IT&T, there's something close, ITT which is not a telecommunications company, but rather a manufacturing company based in Stamford, Connecticut.
Interesting logo, too.
#4 Re: Help Me ! » Planning on studying math for the college entrance exam, need help » 2022-07-15 15:35:01
Hello Zephyr,
Speaking from my experience of running through the education system here in the good ol' U S of A, I can tell you that the vast majority of subjects, topics, and problems were of relative ease to me. Some necessitated a bit of elbow grease, but nothing too much to work out, really.
Your study plan's time schedule sounds robust to me, and I'm glad that you have the resources to acquire a tutor to help you work the more convoluted topics out. That'll no doubt bolster your understanding and your aptitude at using the tools in your mathematical repertoire.
Good to know the test structure has stayed (roughly, it sounds anyways) similar for the past couple of years. Should help you plan for any bumpy roads ahead.
As for grades 5-8, speaking from my experience as before, there wasn't any serious reviewing that I needed to do for more advanced topics. You can allocate some time to those areas, but hopefully not too much.
About recommendations for additional websites/resources that would (hopefully, anyways) prove particularly productive for your mathematical journey, I'd suggest going through some AMC problems—in case you don't recall, they're artfully and shrewdly-written competitive math problems that are given to kids in middle/high school—from the past. In particular, I'd propound you to look through the AMC 12/AIME exams, hosted by the great folks at AoPS(Art of Problem Solving).
The folks at AoPS also have a thriving, expansive community forum packed with a plethora of deftly crafted math problems that'll surely hone your skills.
BTW, I was going to recommend Brilliant.org, but I've perused through the website and they've... decided to obliterate the community section(which, at least last time I checked in mid 2017-early 2019, was thriving with amiable conversations and a plethora of astute people writing some rather perspicacious problems and eloquently-written wiki articles. Seems like they removed the community section for some rather farcical reasons(presumably in an avaricious pursuit of profit, which is frankly rather sad.)
They also have an extensive YouTube channel w/ the one and only Richard Rusczyk, where he dives into those aforementioned AMC problems and solves them while laying out his thought process to help others with his impressive insight. Here's a representative example involving some 3D geometry—which you mentioned was important.
As for what topics I would focus on, I'd lean on 6(Vieta's formulas), 12(Exponentials, to some extent), 16(Logarithms, again to some extent), 19(Arithmetic and geometric progressions and sequences, which can get tricky. Although Brilliant's shamefully removed their community section, their wiki, written mainly by the aforementioned community, is still rather excellent. Check out the wiki articles about arithhmetic progressions and geometric progressions.), 20(Combinatorics can also get messy fast), 23(Planimetrics involving triangles, circles, and quadrilaterals. Personally I've never heard planimetrics outside of a real-world engineering context, but just through the catch-all term of "geometry". But yeah, I'd really invest some time there. Personally, geometry was never a point of particular ease for me—there'd always be some deception just around the corner(pun not intended)), and last but certainly not least, 24(Stereometry / Solid geometry. If you thought 2D geometry was a colossus of catastrophe... 3D geometry is... one more dimension of perplexing, intricate nonsense to deal with. At least for me, I'd definitely consider allocating quite a bit of time there.)
For the scoring system there, that'd be typical in most high school exams involving you to write out your work.
Also, I don't think (but it's been a while anyways) that you can reply to your own posts as a guest. Try registering up on this storied forum!
In any case, good luck on your circuitous but (hopefully) rewarding journey!
#5 Re: Help Me ! » Quadratic equations » 2022-07-04 09:04:28
Heya Jade,
I'm going to answer this thread(and not the other one, as the details appear to be the same.)
To determine when the ball hits the ground, solve the equation when h equals 0.
You can either complete the sqiare or use the quadratic formula. For the sake of simplicity, I'm going to proceed using the latter method, but either one is fine.
For a quadratic equation
the roots are
So plug in the relevant coefficients, and solve as follows:
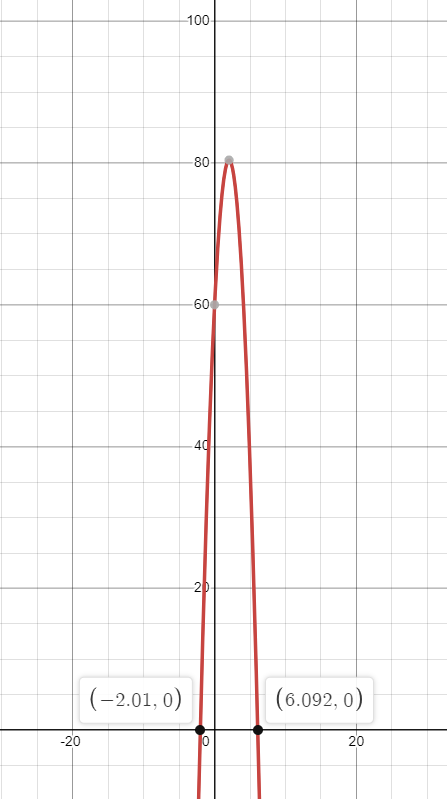
You get . The negative solution obviously doesn't make sense, so strike it out, and you're left with the actual answer, 6.092 seconds.
Here's a useful graph visualizing the vertical elevation of the ball through its flight with the two roots of the equation.
#6 Re: Maths Is Fun - Suggestions and Comments » Bring back the infinity favicon for this website » 2022-06-28 02:21:01
Editing posts after they have been posted does not make them acceptable. Ive seen that done on other boards and I maintain that the original
The Edit feature is there for a reason. I merely added some images to clarify what I was saying. And I think my post is plenty acceptable.
#7 Re: Maths Is Fun - Suggestions and Comments » On improving the "Messaging" subsection of the Profile section » 2022-06-27 03:15:10
Hi,
I know this is a bit of an aside but still - it's surprising how dynamic the world of the internet is.
Personally, I've never heard of these services mentioned above, with the sole exception of AOL, which we use as an inside joke among my friends to describe someone who just can't move on from the old, lives in a shed with a cowboy hat - that sort of thing.
Today's mega giants - Discord, Reddit, YouTube, Instagram, Twitter even outlook or gmail! How long do they have?
I was a five year old when Skype and Yahoo were all the rage. Why did they stop? Why do any of these stop?
Is there a way to determine the decline of a certain app or website?
What are the factors behind this?
Yeah... looking back at the "old" Internet, personally, I miss the old, more decentralized web, not dominated by a couple of massive tech conglomerates, w/ the increasing superficiality, the vapidity of modern dialogue accelerating an ever-faster pace.
As for the mammoths of today, I have to say that barring a major scandal involving those services, I don't see them going away in terms of dominance in the next 3 years(granted, things can change, but prob not that fast.)
And for an alternative browser rising up and for being somewhat competitive in terms of marketshare w/ Chrome? Probably not happening, unless major funding comes to Mozilla and Firefox w/ Gecko, the only other viable browser engine.
#8 Maths Is Fun - Suggestions and Comments » Bring back the infinity favicon for this website » 2022-06-19 08:55:06
- Mathegocart
- Replies: 2
Hello MathIsFun Forum people,
I recall(or perhaps my memories are faulty) that this forum website used to feature an infinity favicon(for those not in the know, a favicon is a small image that is displayed before the page title in the browser tab)![]()
An example of a favicon, using the Wikipedia article on Book. Browser used is Chrome 102.0.5005.115 on Windows 10.
However(perhaps occurring after the forum update), the favicon is now missing. This makes it somewhat difficult to differentiate the tab amongst a crowd of other tabs, as you may understand. Adding back the favicon would facilitate distinguishing the tab amongst various other tabs.![]()
If you find this enough of a problem as I do, then perhaps you'll find my client-side userscript(a piece of JavaScript that facilitates and augments a website to improve or otherwise add a myriad of features) helpful - it simply adds a link tab w/ a rel parameter for the image to the <head>, hosted on postimage, thus adding an infinity favicon to the MathIsFun forum.
To apply this favicon, use a userscripts manager, such as TamperMonkey(which was open source for a long while until 2018, when the developer pushed it under a propietary license... which is disappointing to say the least) or ViolentMonkey, which is fully open source. Both are cross-browser, so feel free to use them on your browser of choice.
// ==UserScript==
// @name MathIsFunFaviconAdder
// @namespace na
// @version 0.1
// @description Interim solution for the sudden lack of a favicon on the MathsIsFun forum website.
// @author Mathegocart
// @match https://www.mathisfunforum.com/*
// @icon https://i.postimg.cc/tTMvdx7c/infinity-icon-64.png
// @grant none
// ==/UserScript==
'use strict';
(function() {
var link = document.querySelector("link[rel~='icon']");
if (!link) {
link = document.createElement('link');
link.rel = 'icon';
document.getElementsByTagName('head')[0].appendChild(link);
}
link.href = 'https://i.postimg.cc/tTMvdx7c/infinity-icon-64.png';
})();And here's the final result... ![]()
P.S. I wish that the [_code_] tag had language-specific highlighting, like [_code lang=js_]... that would improve readability greatly. (The underscores are there to stop the BBCode parser from stopping me from posting this.)
Example of a code highlighting example with js and the style atom-one-dark on the highlight.js website
#9 Re: This is Cool » Library of Babel » 2022-06-18 19:37:32
I think you could. My 'Mycroft' has been working on this sort of thing since he graduated. Try googling the School of Informatics, University of Edinburgh.
Bob
I've got the university, but what specifically are you referring to?
#10 Re: Maths Is Fun - Suggestions and Comments » On improving the "Messaging" subsection of the Profile section » 2022-06-13 02:11:56
hi Mathegocart
I cannot find a way to edit this using my admin access.
Bob
Hopefully MIF himself might intervene if he has time. I always thought that the "Messaging" subsection of the Profile section was quite archaic... some aspects do need to change sooner rather than later!
#11 Maths Is Fun - Suggestions and Comments » On improving the "Messaging" subsection of the Profile section » 2022-06-12 14:04:36
- Mathegocart
- Replies: 4
Hello MIF friends,
While I was browsing through my Profile, I was noticing that the "Messaging" section's options are, unfortunately, a little anachronistic:
Jabber is a (not too popular these days) instant messaging service that runs on XMPP - which doesn't have the widest appeal(to my chagrin) these days.
ICQ also is antiquated w/ not too much popular at around 11 million monthly users(compare to 150 million for Discord, the main IM platform of the day).
Microsoft Account is fine, though Skype waned substantially in popularity w/ the pandemic and Zoom.
AOL IM was the premier messaging service of its day(late 90s to early-mid 2000s), but it was (sadly) infamously discontinued by AOL on December 15, 2017. RIP AIM. Though it appears as though that someone has rekindled it, albeit with nowhere near the amount of users that AIM had.
Last but not least, Yahoo! Messenger was one of the great message titans of its day as well, but after being shortly reintroduced in 2015, it was shut down entirely on July 17, 2019, replaced with a new service known as Yahoo! Together(which bore a suspicious resemblance to Slack.) Unfortunately, that was shut down as well on April 4, 2019. Yes, Yahoo! Messenger has been throughquite the journey.
In this day and age of the fast-changing Internet, we ought to recognize the current IM behemoth of the day, Discord - which boasts, according to some estimates, 150 million active monthly users.
Please add Discord as an option in the Messaging subsection of the Profile subsection.
#12 Re: Puzzles and Games » Hangman 1 » 2022-06-12 13:28:41
Yes, it’s quite clear by reading the old posts that this very forum used to be a rather vibrant and lively place.
Take your time about the celebration…it’ll be worth it!
No ‘e’? Well, then, how about ‘a’?
And, indeed, I do remember the glory days of this storied forum, with many shrewd, whimsical, and ingenious people who contributed greatly to the forum... sadly, some have left this forum for reasons unspecified. Though there is a general trend towards a more centralized, superficial Internet dominated by the tech giants at hand, hence the recent downfall of most forums. But I still have quite a penchant for forums.
As for the word... nope, nothing there either.
Word: _ _ _ _ _
#13 Re: Puzzles and Games » Hangman 1 » 2022-06-11 16:55:08
I'd be worried if anyone remembered a word after that long, because that'd mean they had nothing better to do!
I'm looking forward to your celebratory post!
Is there an 'E' in your word?
Hey CurlyBracket,
Haha, I suppose you are right. In the previous forums where I resided, I kept a running scoreboard of players(sadly the forum has slowed down to a grinding halt bc of incompetent leadership).
As for the celebratory post, I'm going to have to allocate some time and resources to writing up something eloquent and moving, for this vast and prodigious forum has contributed immensely to my personal pursuits, passions, and penchants.
Last but not least, nope, no 'e'!
Word: _ _ _ _ _
#14 Re: Puzzles and Games » Hangman 1 » 2022-06-04 18:57:30
Hey folks! It's been 1 year, 10 months, and 26 days since I last posted my word - and, as you might've guessed, I've forgotten(sorry.) And, we're about to reach a milestone—it's been 9 years, 6 months, and 24 days since I started my Hangman series on this forum—nearly a decade(oh, and it has been more than a decade since I started my account(actually, 10 years, 1 month, and 5 days)... so I'm a bit late and I'll write up an appropriate celebratory post sooner or later!)
With no further ado, let me reveal my new word:
_ _ _ _ _
Good luck to all!
#15 Re: This is Cool » Library of Babel » 2022-05-17 02:20:52
Hey guys,
I really enjoy the nice little philosophical discussion that's revving up around here... although a real life Library of Babel might as well be nonexistent as with all the great fables of literature, one may access a virtual, online library of Babel(which also has an analogous image repository). All the solutions in the world, in one online repository...
#16 Re: Introductions » Hi » 2022-03-29 13:44:33
Hey 0G74,
I oughtta give my welcome. Welcome, 0G74! I hope you will have an amiable time here.
#17 Re: Help Me ! » dividing small number over a larger number concept » 2022-03-13 16:48:29
Hannibal lecter wrote:Bob wrote:++++++++++++++++++++++++++++++++++++
I'm old enough to have used mechanical calculators to do arithmetic.can you please tell me or send me a photo of that mechanical calculators and where to do you have a similar links to buy it from amazon or ebay
And to do division you had to do repeated subtraction.
++++++++++++++++++++++++++++++++++++I couldn't understand how division is a repeated subtraction
++++++++++++
example. If the calculation was 48 divided by 6 you would set up 48 in the register, then set up 6 as the amount to subtract, and then wind the handle backwards so the display showed 42, then 36 then 30 and so on until zero was showing. A side register would show how many times you had turned the handle and it would be showing 8 in the case.
++++++++++++but 48 divided by 6 is 8 directly how could it displayed 42 at first from where did we get this number even in papers couldn't find it
++++++++++++
If the calculation was 1 divided by 8 the procedure was as follows:
Now you are subtracting 0.08 each time.1-
0.8
0.2-
0.08
0.012
++++++++++++
the number is 0.08?? is very ambiguous to me, from where we get that number even in papers I tried a lot I couldn't figure it
you said " subtracting 0.08 each time "and thanks you so much you understand what I want it's really my problem I can't understand division process
Hey Hannibal lecter,
As for the mechanical calculators, this site provides an eloquent and comprehensive overview of their functions and history. There are also some captivating pictures that the site owner has graciously provided.
They're available on eBay(this one appears to be going for $200 including shipping costs where I live.) Can't seem to find any on Amazon though - I'm afraid eBay's your best bet here.
#18 Re: Help Me ! » Rational Functions and Equations Word Problems » 2022-03-02 16:12:55
Hello Not Dav,
Consider
Knowing these two facts, one can construct an equation:
.
Do you know how to solve the problem from there?
#19 Re: Introductions » I'm back! » 2022-02-22 13:24:02
Happy New Years, Jabah! Welcome back.
#20 Re: Help Me ! » Trigonometry Table » 2022-02-03 04:36:02
Hi Bob and ganesh,
Thanks for all the useful links. I tried my best to understand the 'Sine Cos Tan in 4 Quadrants ' part, but I find the fact that they skipped Coordinate Geometry at school is largely preventing me from doing so. So now my plan is to study some of that, and then return to Trigonometry again. I haven't watched the video yet, but I will as soon as I get some time off.
Thanks for your help! I'll reply to this thread if I face any more issues.
Hey CurlyBracket,
Best of luck on your mathematical journey! There might be twists and turns on the way, but it will be genuinely rewarding.
#21 Re: Maths Is Fun - Suggestions and Comments » Possible to report spam members? » 2022-01-16 04:09:36
hi Mathegocart
Admin and Mods check the forum most days and deal with spammers and their posts.
At the bottom of every post you should be seeing a 'Report' button that flags up any post of concern. Admin and Mods get the report message when they log in and can jump to the post and do something about it. Are you seeing that button? Some forum features were lost when we moved to the new server and things that I can see are not necessarily visible to all. So please confirm if you have the report option and try it out by reporting this post for me. You should get a message space to give your reason, so please make it clear it's a test for me.
If you stumble on an edited post that isn't showing as a new post you should still be able to report it.
I've had a look through the options available to me on the forum. I can switch off the information on the post side panel so that a members website doesn't show, but that would have apply to everyone, not just one member. Similarly signatures can be turned off. I'm very reluctant to do either of these as good members suffer along with the bad.
Bob
Thanks for the clarification Bob. Appreciate the hard work y'all do.
#22 Re: Maths Is Fun - Suggestions and Comments » Possible to report spam members? » 2022-01-15 12:00:59
Maybe try reporting the spam posts?
I've noticed some spammers who've attached *ssay promotional services, but never post. I was wondering if those could be reported somehow.
#23 Re: Maths Is Fun - Suggestions and Comments » Possible to report spam members? » 2022-01-15 11:48:25
It is unfortunately not just a recent phenomenon: it has been happening daily since I became a mod here and probably before then too (based on the lengthy ban list). In most cases the decision to delete/ban is straightforward since many of the posters you mention have often already been reported multiple times on places like 'Stop Forum Spam' or otherwise have an e-mail address which a simple google search reveals that they've done the same thing on half a dozen other forums. In other cases it can be much more difficult because some new members will deliberately post something harmless and then edit in a link a few days later, or they might pose as an ordinary member only to start eventually posting ads. These (particularly the former) are generally harder to spot and are less easy to deal with: I generally avoid banning posters unless I have good reason to and prefer to have some evidence of wrongdoing if at all possible but these types are admittedly (somewhat) rarer.
New users have to click on an activation link sent to an e-mail address to register which cuts down the number of spam registrations significantly: without this we would easily have a hundred different spammers a day (this is no exaggeration). As I understand there are also restrictions which prevent most new members (with < x posts) from posting links, which is why we have lots of new daily registrations from spam accounts but of those only a small proportion end up posting ads, and there are also word censors which filter out a few too. Consequently the spam that does make it through is, IMO, annoying but not unreasonably so, given (a) the nature and number of spam posts, (b) the overall forum activity susceptible to clicking on said posts and (c) the administrative resource available. At the moment (a), (b) and (c) are reasonably balanced and therefore the level of spam is, in my view, manageable. Regrettably we have in the past had the occasional new member post some particularly awful content on here -- and I can't be certain that some of the people who visit this forum (members or not) didn't fall victim to it where we may not have been able to deal with the issue immediately -- but fundamentally the most determined spammers/advertisers will find a way around any precautionary measure and so we tend to operate on a best endeavours basis given the tools we have.
In the meantime please continue to report any posts you see like this as it helps us deal with them more quickly: we often check the forum a few times a day but there will always be the odd one or two that get through when none of the mods/admins are active.
Thank you for the extensive and comprehensive response. I appreciate the tenacious efforts you guys pull.
#24 Maths Is Fun - Suggestions and Comments » Possible to report spam members? » 2022-01-14 08:56:02
- Mathegocart
- Replies: 10
Hello MIF friends,
There has been a recent influx of members that only post once and have promotional or advertisement links in their bio or signature.
Would it be possible to report and extirpate these spammers?
#25 Re: Introductions » Hello! » 2022-01-14 08:54:24
Hello Rachael.