Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 Help Me ! » Tangents to 2 circles » 2013-11-25 00:16:58
- jimi70
- Replies: 8
'The circle S1 with centre C1(a1, b1) and radius r1 touches externally the circle S2 with centre C2(a2, b2) and radius r2. The tangent at their common point passes through the origin. Show that
(a1² - a2²) + (b1² - b2²) = (r1² - r2²).
If, also, the other two tangents from the origin to S1 and S2 are perpendicular, prove that
|a2b1 - a1b2| = |a1a2 + b1b2|.'
I can do the first part but need help with the second part.
Thanks for your time.
#2 Re: Help Me ! » Weights on a string » 2013-05-07 22:02:44
Hi bob
Sorry to ressurect this, but can I use conservation of momentum with gravity acting on the sytem? I thought the condition was no external forces.
#3 Re: Help Me ! » Weights on a string » 2013-04-30 00:54:07
bob
Thanks so much. I get that perfectly. As an aside, can I calculate the speed that the heavier weight leaves the floor using conservation of momentum?
#4 Re: Help Me ! » Weights on a string » 2013-04-27 14:07:11
bob,
Can you tell me what is the condition for when the string goes taut?
#5 Help Me ! » Weights on a string » 2013-04-21 22:24:53
- jimi70
- Replies: 10
'Weights of 3 kg and 4 kg are connected by a light inextensible string, which passes over a smooth peg. The system is released from rest. Find the acceleration of the system.
After two seconds, the heavier mass strikes the floor and comes to an instantaneous halt. Find the time before the string is again taut.'
I've worked out the acceleration to be 1.4 m/s/s but I'm not sure about the second part. Can somebody help please?
#6 Re: Help Me ! » coefficient of restitution problem » 2012-11-08 00:53:19
Hi bob
Thanks for checking. I've managed to solve it and you are right; it should be:
(2de^2)/(1+e^2)
It must be a misprint in the book.
#7 Help Me ! » coefficient of restitution problem » 2012-11-05 22:40:37
- jimi70
- Replies: 3
'A small smooth sphere moves on a horizontal table and strikes an identical sphere lying at rest on the table at a distance d from a vertical wall, the impact being along the line of centres and perpendicular to the wall. Prove that the next impact between the spheres will take place at a distance
2de^2/(1 - e^2)
from the wall, where e is the coefficient of restitution for all the impacts involved.'
Before I tried the problem, I tried the formula on an example:
Let:
Ua be the initial speed of sphere a
Ub be the initial speed of sphere b
Va be the speed of sphere a after the first collision with sphere b
Vb be the speed of sphere b after the first collision
I let Ua = 2 m/s, d = 15 m and e = 1/2 and these are my workings:
by restitution:
1/2 = (Vb - Va)/2
Vb - Va = 1
by conservation of momentum:
2 = Va + Vb
so: Vb = 3/2 m/s and Va = 1/2 m/s
This means that sphere b will take 10 seconds to hit the wall and, during this time, sphere a will have travelled 5 m towards the wall. After the impact with the wall, sphere b will rebound with speed 3/2 x 1/2 = 3/4 m/s. Since there is now 10 m between the spheres and they are heading towards each other: 1/2t + 3/4t = 10 where t is time in seconds. This means they will collide after another 8 seconds and this will be at a distance of 6 m from the wall. Using the formula, however, I get 10 m. What am I doing wrong?
#8 Re: Help Me ! » Vector geometry » 2012-06-02 10:19:07
Hi bob
I got the following:
AC = 2/3(-a + d)
CD = 1/3(-a + d)
FE = 3d/5
FG = na
EG = -3d/5 + na
EK = 4/7(-3d/5 + na)
DG = -d + na
but I still don't know what to do next.
#9 Help Me ! » Vector geometry » 2012-05-31 02:39:10
- jimi70
- Replies: 5
I came across this problem the other day. I understand the vectors behind it but don't really have a definite strategy in solving it. My approach is a bit random. Can someone please advise me of the best way to approach it?
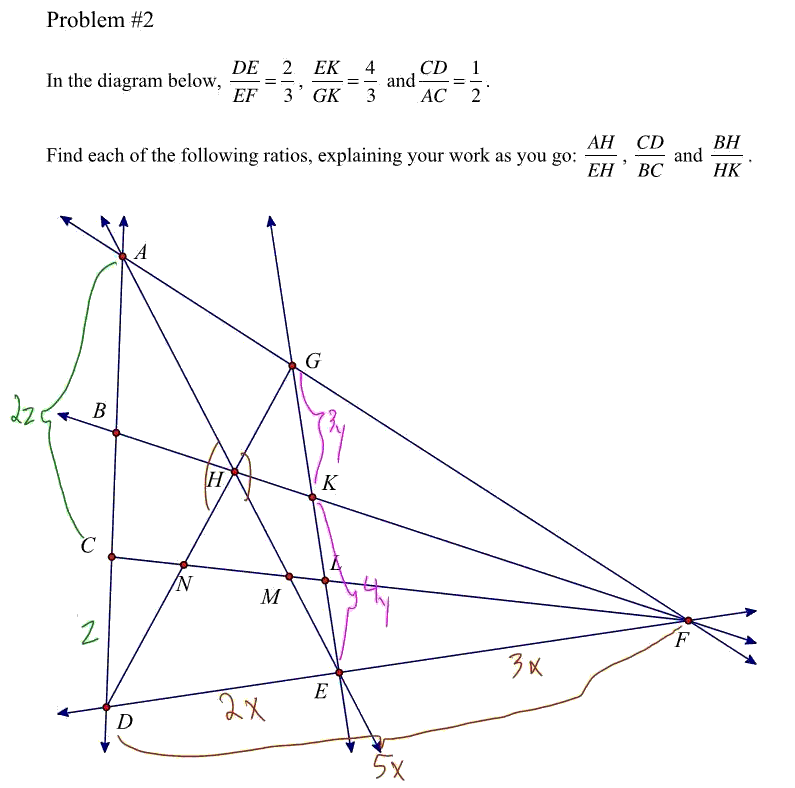
#10 Re: Help Me ! » triangle with vectors » 2012-05-28 23:45:43
thanks again bob, I got all of that. Just one question: was there any particular reason why you chose a as the other vector?
#11 Help Me ! » triangle with vectors » 2012-05-28 04:27:23
- jimi70
- Replies: 3
 [/url]
[/url]
In the diagram, vector OB = b, vector OC = 4b/3 and vector AP = 2/3 vector AB.
Given that vector AQ = m vector AC and that vector OQ = n vector OP, calculate the values of m and n, and the ratio of the vectors AQ:QC.
I can't see how to use the vectors given only and I can't see any similar triangles. Can somebody get me started?
#12 Re: Help Me ! » Block on horizontal plane » 2012-05-28 03:24:16
bob
Just a couple of questions about your second diagram:
Is that right that the friction acting against the top block, Ft, acts in the opposite direction on the lower block?
Shouldn't Fb be acting in the opposite direction? (It's probably my diagram. I'll try and download an image next time).
btw, thanks for all your help.
#13 Re: Help Me ! » Block on horizontal plane » 2012-05-27 22:04:27
bob
sorry again. The 4 N force acts in the left direction of the block.
#14 Re: Help Me ! » Block on horizontal plane » 2012-05-27 21:03:19
bob
sorry, it's my diagram. The 5 N force is supposed to be acting upwards at an angle.
#15 Help Me ! » Block on horizontal plane » 2012-05-26 20:46:28
- jimi70
- Replies: 8
5 N
\ |
\60 deg
\|________
| |
4 N ----- |________|
A rectangular block B of weight 12 N lies in limiting equilibrium on a horizontal surface. A horizontal force of 4 N and a coplanar force of 5 N inclined at 60 degrees to the vertical act on B.
(i) Find the coefficient of friction between B and the surface.
B is now cut horizontally into two smaller blocks. The upper block has weight 9 N and the lower block has weight of 3 N. The 5 N force now acts on the upper block and the 4 N force now acts on the lower block (see diagram below)
5 N
\ |
\60 deg
\|________
|_9 N____|
4 N ----- |_3 N____|
The coefficient of friction between the two blocks is u.
(ii) Given that the upper block is in limiting equilibrium, find u.
(iii) Given instead that u = 0.1, find the accelerations of the two blocks.
my answers:
(i) (4 + 5 sin 60) / (12 - 5 cos 60) = 0.877
(ii) (5 sin 60) / (9 - 5 cos 60) = 0.666
(iii) for the upper block: 5 sin 60 - 0.1(9 - 5 cos 60) = 9a/9.8
so a = 4.01 m/s/s
I don't know how to calculate the acceleration for the lower block as I don't know how the friction between the two blocks affects the tractive force of the lower block. Can somebody help me?
#16 Re: Help Me ! » Pulley and string problem » 2012-05-21 20:32:06
thanks once again bob
#17 Help Me ! » Pulley and string problem » 2012-05-15 20:49:53
- jimi70
- Replies: 2
| O | pulley
| |
| |
! !
O O
A B
Acceleration = 1.4 m s^-2 downwards from particle A
Particles A and B are attached to the ends of a light inextensible string. The string passes over a smooth fixed pulley. The particles are released from rest, with the string taut, and A and B at the same height above a horizontal floor (see terrible diagram). In the subsequent motion, A descends with acceleration 1.4 m s^2 and strikes the floor 0.8 s after being released. It is given that B never reaches the pulley and before A strikes the floor the tension in the string is 5.88 N.
(a) Calculate the mass of A and the mass of B.
(b) The pulley has mass 0.5 kg, and is held in a fixed position by a light vertical chain. Calculate the tension in the chain immediately before and after A strikes the floor.
(a) for A: mg - 5.88 = 1.4ma so m = 0.7 kg
for B: 5.88 - mg = 1.4ma so m = 0.525 kg
I need help with (b). I would've thought we could just take the weight of the particles and the pulley, i.e. (0.5 + 0.7 + 0.525) x 9.8 = 16.905 N but this doesn't equate to the sum of the weight of the pulley and the tensions in the string, i.e. 0.5 x 9.8 + 2 x 5.88 = 16.66 N
Why is there a difference?
#18 Re: Help Me ! » Ring threaded on string problem » 2012-05-07 23:53:46
bob
Sonething just occurred to me. If the string is not now taut, does that mean that we cannot tell exactly how far the string will hang below B?
#19 Re: Help Me ! » Ring threaded on string problem » 2012-05-05 22:19:13
Thanks bob.
for (a) T sin a + T sin b = 14
sin a = 0.24/0.4 = 0.6
sin b = 0.24/0.3 = 0.8
so: 1.4T = 14 and T = 10 N
T cos a - T cos b = W
cos a = 0.8
cos b = 0.6
so: 8 - 6 = W and W = 2 N
'The total length of the string is 0.7 and AB is 0.24.
So there must be 0.46 m to account for.'
Sorry, it's probably my awful diagram, but AB must be 0.5 m. That means that there will be 0.2 m to account for. Does that mean that R will hang 0.1 m below B?
#20 Help Me ! » Ring threaded on string problem » 2012-05-04 20:34:21
- jimi70
- Replies: 5
A smooth ring R of weight W N is threaded on a light inextensible string. The ends of the string are attached to fixed points A and B, where A is vertically above B. A horizontal force of magnitude P N acts on R. The system is in equilibrium with the string taut; AR makes an angle a with the downward vertical and BR makes an angle b with the upward vertical (see diagram below).
A
| -
|a -
| -
| - R --------->P N
| b -
|-
B
It is given that when P = 14, AR = 0.4 m, BR = 0.3 m and the perpendicular distance of R from the vertical line AB is 0.24 m.
Find:
(a) the tension in the string;
(b) the value of W.
For the case when P = 0,
(c) describe the position of R,
(d) state the tension in the string.
It's the last 2 parts that I'm struggling with.
Thanks for any help.
#21 Re: Help Me ! » Reaction forces problem » 2012-04-05 06:56:12
Thanks bob
Yes, I'm pretty sure now that you're right, i.e. 'total reaction' in the question is the resultant of the normal reaction and friction.
#22 Help Me ! » Reaction forces problem » 2012-04-04 00:48:07
- jimi70
- Replies: 2
A particle of mass 0.5 kg is moving at constant speed on a rough horizontal table in the direction of the constant unit vector i. The particle is acted on by three forces, namely (i) its weight, (ii) an appiled force P and (iii) the total reaction of the table R. Given that P = (3i + 8j) N, where j is a unit vector vertically downwards, and taking g = 9.8 m s[sup]-2[/sup], determine R in the form R = (ki + lj) N, where k and l are numbers. Hence determine the coefficient of friction between the particle and the table, to 2 decimal places.
Now, the part I need clarification on is the part where the question asks for R in the form (ki + lj). I thought that the normal reaction always acted perpendicularly to the surface of contact, in which case there would be no horizontal component, i.e. k would be zero. My book disagrees. Am I confused or missing something?
Pages: 1