
Welcome to the forum.
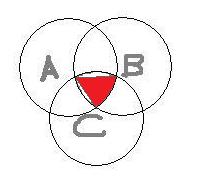
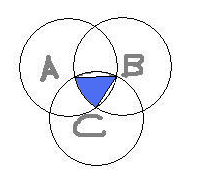
The circles have equal radii, so the triangle formed by the three circle intersection points is equilateral, ie. has angles of 60.
The area of a whole circle would be pi r squared, and a 60 sector is 1/6 of this.
Bob
]]>


This is also the area of the sector bounded by the radii BA and BC and the arc CA in the circle with centre B (blue area in diagram below) and that of the sector bounded by radii CB and CA and arc AB in circle with centre C (green area in diagram below).
Now add up all these areas. You get
. But this actually counts the area of triangle ABC three times. So we must subtract twice the area of the equilateral triangle ABC, which is .Hence the area of the shaded region is
.]]>Nevermind.
What is: "(Pi - _/3)"???
]]>Forgot to send an image of the circle....

Three equal circles with radius r are drawn as shown, each with its centre on the circumference of the other two circles. A, B and C are the centres of the three circles. Prove that an expression for the area of the shaded region is:
A = r^2 / 2 (Pi - _/3)
I couldn't even start to attack the question ![]()