The Conway Polynomial
The Conway polynomial is a polynomial invariant of knots and links described by the following three axioms:
Axiom 1: For each oriented knot or link K there is an associated polynomial ∇[sub]K[/sub](z) ∈ Z[z] (Z[z] is the ring of polynomials in z with integer coefficients). If one knot K is ambient isotopic to another knot K' ( K ~ K'), then ∇[sub]K[/sub] = ∇[sub]K'[/sub].
Axiom 2: If K is ambient isotopic to the unknot (K ~ O), then ∇[sub]K[/sub] = 1.
Axiom 3: Suppose that three knots or links K[sub]+[/sub], K[sub]-[/sub], and L differ at one crossing in the manner shown below:
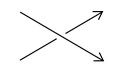 K[sub]+[/sub]
K[sub]+[/sub]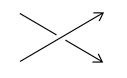 K[sub]-[/sub]
K[sub]-[/sub] L
L
Then ∇[sub]K+[/sub] - ∇[sub]K-[/sub] = z∇[sub]L[/sub].
Axiom 1 tells us that for any knot or link there exists a Conway polynomial; Axioms 2 and 3 give us a way to find it. Tomorrow I shall post an example of how to use these axioms to find the Conway polynomial of a knot (using a specific example, most likely the trefoil, but maybe some others), and perhaps I shall also describe the Jones polynomial, the HOMFLY polynomial, the chromatic polynomial, and more.
Edit: Wow, sorry about that, I could have sworn this topic had been replied to very recently, and I didn't realize it had been moved from the formulas section.
]]>