At first, I assumed the formula for arc length of a polar curve was the integral of r dθ, from a to b. This will work for a circle and a similar method will work for area but not for a spiral or any polar curve when the radius is changing. As the change in the radius has an effect on its direction at a given point.
Today I devised a new formula shown in the drawing below.
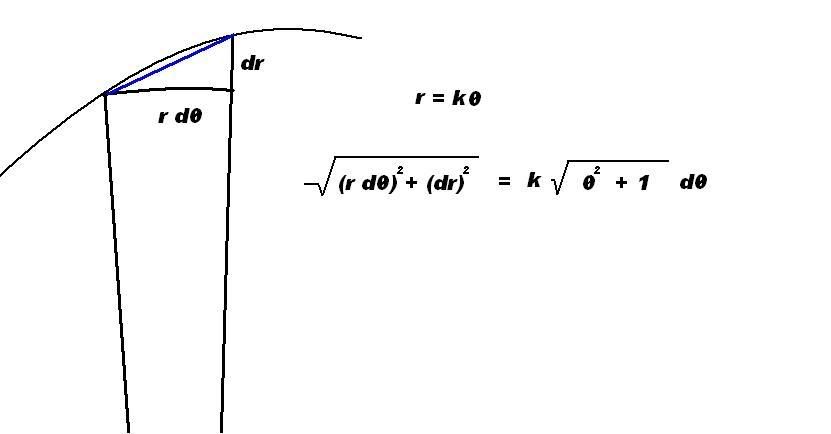
It basicly forms a right triangle. As dθ approaches zero, it tends to become a right triangle with a flat bottom. This seems a logical formula to me but technically, unlike the tetherball situation, the path of the line is not exactly hinging around the origin. Like the path of a straight line expressed in polar form. The path is definitly not hinging about the origin.
But anyway, the equation of a spiral is r = kθ, replacing kθ for r and k dθ for dr in the expression I had, and with a little factoring you can rearrange it into the form k sqrt (θ^2 + 1) dθ. This can be integrated using a trig sub but its a real nasty one. In the end the integral of sqrt (θ^2 + 1) dθ is:
k [ (1/2 ln | sqrt ( dθ^2 + 1) + θ | + 1/2 θ sqrt ( θ^2 + 1) ]
I decided to define the value of k in the spiral function:
r = θ * h/2pi this will increase the radius by the constant h once every rotation. (so k = h/2pi)
I let h = 1/8 so the radius increases by 1/8 every rotation. I then allowed it to rotate once, starting from one when the radius = 1, which is 16 pi. So 16pi to 18pi. I got a value of 6.67705. This makes sense, begining with a radius of 1 and increasing 1/8 every turn, it should be a little more then 2pi.
I then wrote a program to use the distance formula and plotting 10,000 points on the curve and summing the distance between each one. I got 6.67705 on the nose. The exact same amount! ![]()
However, I tried dividing it into 100,000 points and for some reason the sum started getting smaller. As the number of intevals on the curve increases, the total should increase. (the shortes distance between two points is the line that connects them) it should increase and approach a certain value as a limit, but never decrease. So thats most likely the compiler being unable to hold super small numbers to many decimal places.
(edit) Allriiiight I just increased the number of rotations to 10 and the two answers are still exactly the same. I figured if there's a slight inaccuracy it will begin to show better with more rotations.
]]>