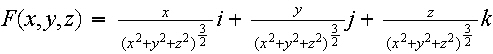
is a vector field. Now how do I evaluate the line integral F.dr in the region C where C starts at the point A(12,0,0), ends at point B (0,12,5) and is an arc on the helix:
x=12cos πt
y=12sin πt
z=2t
where π is the number pi.
I know how to evaluate line integrals for a helix and using F but now with the points added in (point A and B) I have no idea how to begin. Please help.
]]>