Take, in my opinion the greatest single contributors to mankind's knowledge, the Greeks for example. They created a slave system so that they could spend all of their time in "noble" pursuits such as the journey toward enlightenment. Euclid never "worked" a day in his life. All he ever had to do was contemplate new ways to view form and mathematics. In fact, "working" was regarded as dishonorable for a long period of their civilization, as it was viewed as a waste of human potential to understand truth.
Maybe sometime in the near future we will have the technology to take care of the mundane aspects of existence so that we too can focus our energy into mental and spiritual pursuits.
]]>They just don't make geniuses like they used to.
One thing i'd like to know is how pi was discovered. And why the area of a circle is the integral of the circumfrence. WIERD!
]]>I love calculus....
And thanks for giving me such a fun problem. Solids of rotation are really awsome problems in my opinion.
]]>Of course if I'm an ancient greek god thats fine with me. Fear me...
]]>Once again, this forum has produced a neat little formula for all that have the pleasure of reading it.
Thanks again, mikau.
V(h) = πh²/3(3r - h).....sweeet!
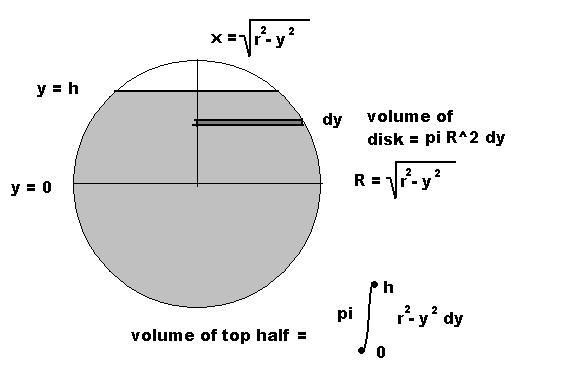
]]>Here you go! Volume as a function of height:
V(h) = pi ( r h^2 - 1/3 h^3) where r is the radius of the sphere and h is the height of the "water" measured from the bottom of the sphere. (ie. if the sphere were filled to the top, h = 2r)
Lets check. The formula for the volume of a sphere is 4/3 pi r^3, if radius is 1 the volume should be 4/3 pi. Now lets use my formula. if the sphere is filled with water the height of the water from the bottom of the sphere will be the diameter or 2r. The radius in this case is 1 so h is 2. Fill in these values and you get:
pi ( (1) (2)^2 - 1/3 (2)^3) = pi (4 - 8/3) = 4/3 pi same answer!
This time lets let h = 1. The volume will only be half. So it should come out to 2/3 π
pi ( (1) (1)^2 - 1/3 (1)^3) = pi( 1 - 1/3 ) = 2/3 pi. Again the correct answer!
It works! :-D This was fun!
]]>I might be doing something wrong but I integrated the function you have above and I got:
π [ ry - y³/3 ]
If r = 1 and h(upper) = 2 then this equals -2π/3
I'm not ripping, I liked your thought process too. It just doesn't seem to work in this instance.
edit!!
I didn't see that you were using the equator as the x axis.
]]>But the disk method: ∫πf(y)²dy rotates about the x axis while the shell method ∫2πxf(x)dx rotates about the y axis. The two I would think are incompatible.
forgive me if I'm wrong but isn't the disk method integrated in terms of x when rotating about the x axis?
]]>