Anyways, all we're concerned about is the ratio, so we can assign values to either the circle or the square (but not both) and find the area of the other in terms of the first.
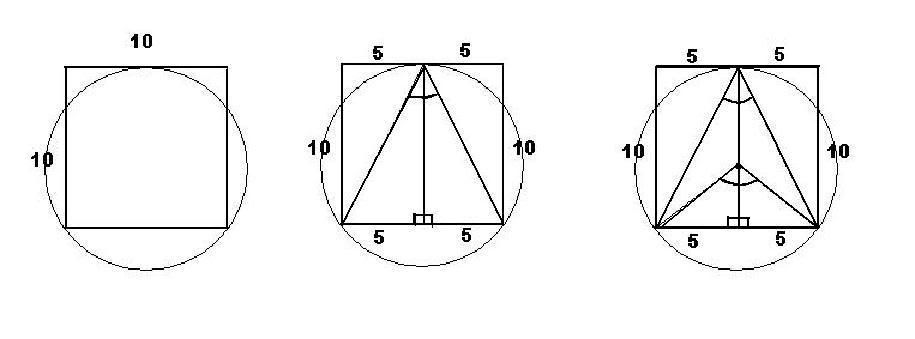
Lets start by letting the square be 10 by 10. If we divide it in two and draw diagonals, we have drawn an inscribed angle inside the circle. The length of this incribled angle is 2 arctan(5/10) thus the measure of the intersecpted arc will be 4 arctan(5/10). We can now draw an angle from the center of the circle to the edges of this arc to find the middle angle. Divide it by 2 to find the angle of a right triangle with a leg of 5. We can now find the radius using trig and solve the problem. :-)
]]>