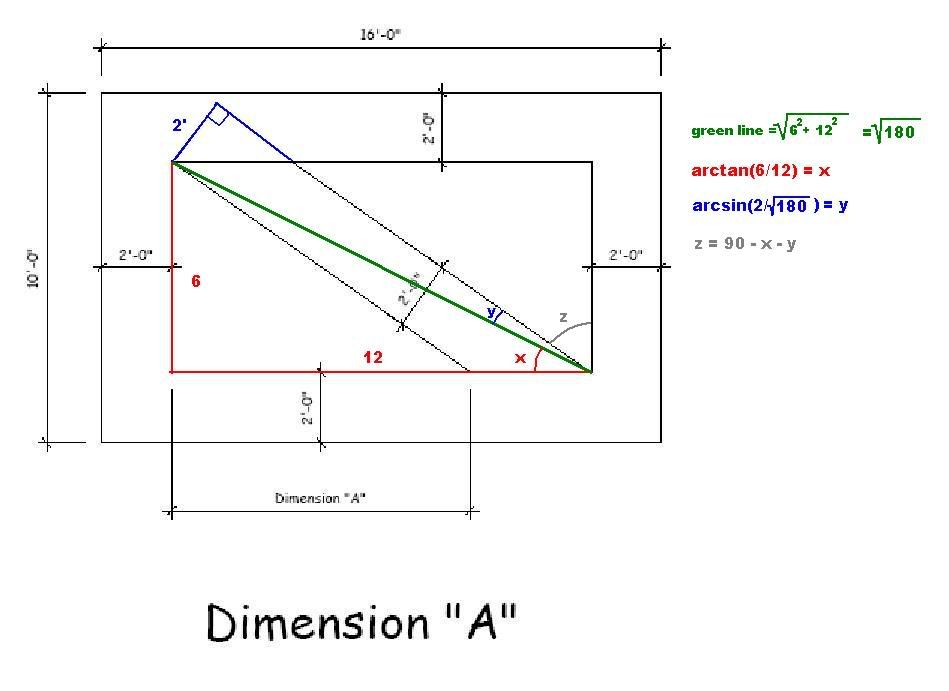
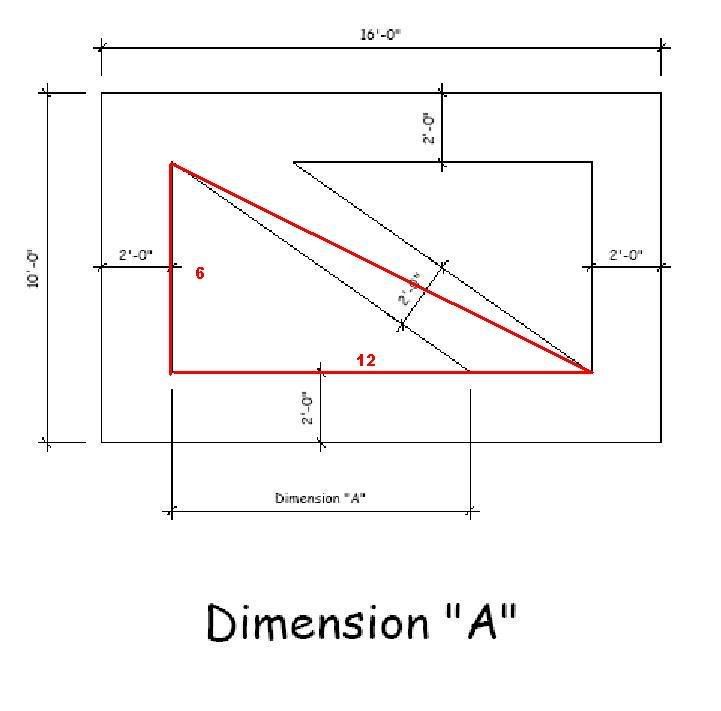
Triangle on the left is triangle A, triangle on the right is triangle B. Angle x is at the top of triangle A and angle y is at the bottom right of triangle A. I have to assume both triangles are similar, so angle x is also at the bottom of triangle B and angle y is at the top left of triangle B.Draw a line from the point of angle y in triangle B to the hypotenuse of triangle A, such that it hits the hypotenuse at a 90 degree angle. Then, draw a line which connects the very top of triangle A to that of B. Call this new triangle, triangle C.
The bottom most angle of triangle C is 90 degrees. Since the hypotenuses in triangles A and B are parallel (assumed), the top left angle in triangle C is equal to angle y in triangle B. Now add the top right angle of triangle C, the 90 degree angle just to the right of it, and angle y in triangle B. Since all these angles put together form a line, they add up to 180 degrees. But we also know that x + y + 90 = 180. Thus, the top right angle in C is equal to angle x. Therefore, triangle C is similar to triangle B and A (assuming these two are congruent).
However, we know that the side of triangle C is 2'. Since the triangles are similar: 6 / 12 = 2 / x, 6x = 24, x = 4. So the other side of triangle C is 4'. This means the hypotenuse of triangle C is about 4.47'.
The length of the entire bottom is 12 feet, 12 - 4.47 = 7.53'.
]]>
![]()