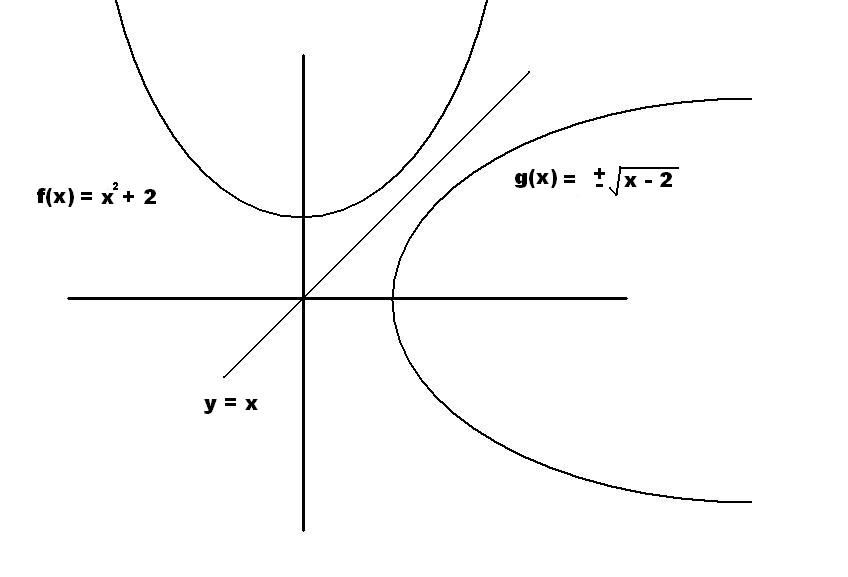
technically g(x) is not a function as a function only returns one value for a given input. It does not pass the vertical line test and does not qualify as a function. I just drew it that way to illustrate how the reflection works.
]]>
technically g(x) is not a function as a function only returns one value for a given input. It does not pass the vertical line test and does not qualify as a function. I just drew it that way to illustrate how the reflection works.
]]>if g(x) is the inverse of f(x) then g(f(x)) = x I can't think of another way other then maybe doing it backwards: f(g(x)). Both will give you x if they are inverse functions.
I think I remember reading something about decomposing functions, I'll take a look.
]]>So inverse function must have 2 different values at point y.
To reduce this we need to use only positive x in the first function.
]]>1)What are two different ways one could determine if one function is the inverse of another?Give an example of each way.
2)Explain why the inverse of a quadratic function is not a function?What do we do to ensure that the inverse of a quadratic is a function?Give an example.
thanks in advance...
]]>