This was also my solution but it seems there is a polygon with fewer sides that meets the criteria.
Why, of course! A concave decagon.
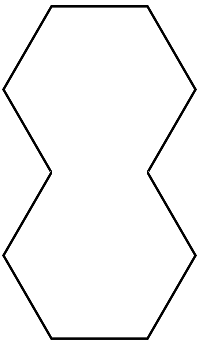
NB: I think Ive proved that a regular concave polygon (i.e. a polygon with equal sides and internal angles either θ or 360°−θ, at least one of which is reflex) must have at least 9 sides. If my proof is correct, it remains to check whether there exists any regular concave nonagon.
]]>I reckon the 5 pointed has 10 sides
]]>What is the regular concave polygon with the smallest number of sides?
All its sides must be equal and all its internal or external angles must be equal as well (i.e. all its internal angles must be either equal or negative, that is, either θ or -θ).
I think its a concave dodecagon

I don't think any regular polygon can be concave
Do you want me to prove it?
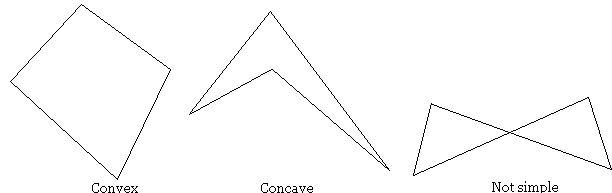 ]]>
]]>You can show that a triangle is never concave using the angle sum property
]]>