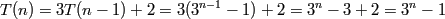
How did you get rid of the n-1 in that step?
]]>If you times by another 3 you just increaase the power by 1 ie (n-1) becomes n.
Bob
]]>It's just a matter of multiplying out the bracket( by 3)
Bob
]]>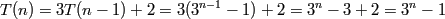
How did you get rid of the n-1 in that step?
]]>k=1
But you want T(1) = 2 ???
Let's see what is happening here.
term to term rule:
so if T(1) = 2
T(2) = 3x2 + 2 = 8
T(3) = 3x8 + 2 = 26
T(4) = 3x26 + 2 = 80
........................
So did you mean
Try again k=1
That's better.
Now for the induction step
assume
use the term to term rule
This has the right form, so the induction step is complete.
Bob
]]>Hi, I am stuck on the last step. What am I supposed to do now?
Problem: Let T(n)=3T(n-1)+2, T(1)=2. Prove by induction that T(n)=3^(n-1)
Here is what I have so far:
Show base case k=1: T(1) = 3^1 - 1 = 2
If T(1) = 2 and if the proposed formula is as you've posted, then T(n) for n = 1 is 3^(1-1) = 3^(0) = 1, not 2. So the base step fails.
You appear, in your work, to have used a different formula from that which was proposed. Is there perhaps a typo somewhere? ![]()
Problem: Let T(n)=3T(n-1)+2, T(1)=2. Prove by induction that T(n)=3^(n-1)
Here is what I have so far:
Show base case k=1: T(1) = 3^1 - 1 = 2
Show for k=n-1: T(n-1) = (3^((n-1)-1)) -1
Show for k=n :
3((3^(n-2)) - 1) + 2