Suppose f1, f2, and g are arbitrary functions of real variables.
Let
f(x) =
f1(x) if x is rational,
f2(x) if x is irrational.
What software can be used to define f(x) such that we can plot y = f(g(x)) directly?
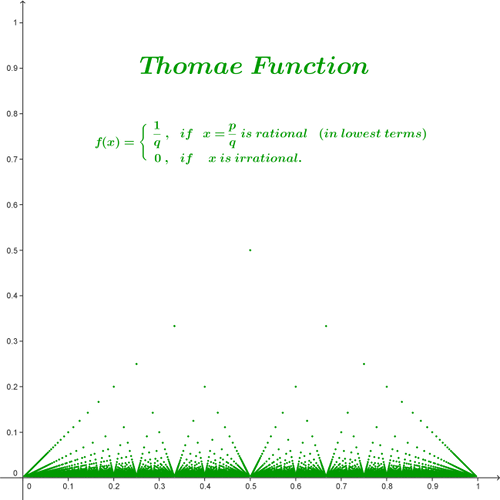
For example, consider the Thomae function:
f(x) =
1/q if x=p/q is rational, gcd(p,q)=1 and q>0,
0 if x is irrational.
How to define f as a function such that we can plot y = f(sin(x)) directly?