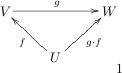
This construction arose because we were treating the space
as a fixed domain. We are, of course, free to treat as as fixed codomain, like this.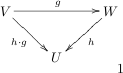
This seems to make sense, certainly domains and codomains come into register correctly, and we easily see that .
Using our earlier result, we might try to write the operator
, but something looks wrong; is going "backwards"!Nothing daunted, let's adopt the convention
. (We will see this choice is no accident)Looking up at my diagram, I can picture this a pulling the "tail" of the h-arrow back along the g-arrow onto the composite arrow, and accordingly (using the same linguistic laxity as before), call
the pull-back of , and make the definition: defines the pullback(Compare with the pushforward)
This looks weird, right? But it all makes beautiful sense when we consider the following special case of the above.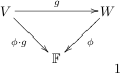
where I have assumed that
Putting this all together I find that, for
I will have as my pullback.I say this is just about as nice as it possibly could be. What say you?
]]>